汪 鑫

（国网四川省电力公司检修公司特高压直流中心，四川 成都 610036）

1 综合能源系统多时间尺度低碳调度优化

1.1 源荷不确定性分析

随着运行时间的改变，风能与负荷的预测偏差呈现逐步下降趋势[1]。本文通过三角模糊数分析风能与负荷的预测偏差带来的不确定性问题。模糊变量计算公式为

式中：为日前风能预测的模糊变量；为日前负荷预测的模糊变量；PWDA,t为日前时间点t风能的预测结果；PLDA0,t为忽略电价响应影响的负荷预测结果；δ3DA为日前风能预测误差区间的上边界系数；δ1DA为日前风能预测误差区间的下边界系数；q3DA为日前负荷预测误差区间上边界系数；q1DA为日前负荷预测误差区间的下边界系数。

设为风能日内预测的模糊变量，为负荷日内预测的模糊变量，为实时阶段的风电模糊变量，为实时阶段的负荷模糊变量。采用与风能、负荷日前预测的模糊变量同样的方法来确定风能、负荷日内、实时预测的模糊变量，具体不再赘述。

当综合能源系统采用分时电价策略后，用户会产生激励响应。因此，引入响应弹性中的预测误差，实现负荷侧不确定性的全面分析[2]。基于消费者心理学模型，利用死区、线性区、饱和区反映不同时间点负荷转移性，并充分分析负荷转移率误差区间[3]。

峰谷负荷转移率可描述为

式中：Δppv为峰谷负荷的电价差；Δppv0为死区边界的电价差；Δppv,max为饱和区电价差；κpv,max为的潜力极大值；αpv为在线性区发生改变的斜率；为误差区间。

当Δppv发生改变后，随之变化，其曲线呈先上升后下降变化。

可描述为

式中：Δppv,max为峰谷负荷转移率误差的极大值 ；为峰谷转折点处的电价差值；αa为电价作为响应误差主要决定因素在前峰谷电价差波动时的响应误差区间系数；αb为电价作为响应误差主要决定因素在后峰谷电价差波动时的响应误差区间系数。

在全面分析负荷预测偏差和分时电价策略各时间点负荷转移引发的不确定问题的基础上，对日前、日内、实时优化控制阶段的各时间点负荷进行拟合分析[4]。其中日前各时间点负荷的拟合可描述为

式中：PLDA0,t为日前时间点t下只衡量预测偏差时的负荷模糊变量；p为波峰时间点负荷集合；f为平峰时间点负荷集合；v为波谷时间点负荷集合；、、为引入响应误差后各不同时间点的负荷转移率；PLDA,pav为日前波峰时间点负荷预测结果的负荷均值；PLDA,fav为平峰时间点负荷预测结果的负荷均值。

此外，用表示日内优化阶段的负荷拟合结果，用表示实时优化阶段的拟合结果，同日前各时间点负荷的拟合描述类似，不再赘述。

1.2 低碳优化调度模型

1.2.1 日前优化调度模型

相隔1 h对综合能源系统进行一次日前优化控制，调度周期为24 h，以便得到各机组未来一日的发电计划。对风力发电、负荷的预测误差和分时电价策略引发的不确定性进行综合分析，将最小化日运行费用作为目标，实现其日前阶段的优化，可描述为

式中：H1为购电费用；H2为天然气购用费用；H3为弃风费用；H4为碳排放费用；Be(t)为时间点t分时购电单价；Pcha(t)为功率；Bg(t)为分时购气单价；Vcha(t)为分时功率；Fng为天然气热值；T为总优化调度时间；Nw为风电场景数量；ρw为弃风费用系数；Pycwt为风电出力预测值；Pwt为实际输出功率；Re为每单位碳排放的购买/售卖价；Ni为化石燃料发动机总数；μi为第i台发电机单位功率下的碳排放大小；ϑi为单位有功功率下的碳排放量。

综合能源系统运行需遵循各设备的实时运行限制条件和爬坡限制条件，同时要符合负荷平衡限制[5-6]。约束公式为

式中：Ppv(t)为时间点t光伏机组的有功功率；Pwt(t)为实际输出功率；Pmt(t)为微型燃气轮机电功率输出值；Pcha(t)为功率；Pedis(t)为输出功率；Pech(t)为蓄电池在进行电能储备时的功率；Pp2g(t)为p2g 设备输入的电功率；Peb(t)为电热锅炉耗电功率；Le(t)为电热锅炉提供热能供应时需要的电负荷；Vcha(t)为分时功率；Fp2g(t)为p2g 设备有功功率输出值；Pgbis(t)为储气罐的放气功率；Pgch(t)为储气罐的充气功率；Vgas(t)为天然气耗用功率；Lg(t)为电热锅炉提供热能供应时需要的气负荷；Qmt(t)为微型燃气轮机有功热功率；Qeb(t)为电热锅炉提供热能供应时的热输出功率；Qhdis(t)为热输出功率；Qhch(t)为储热罐的充热功率；Lh(t)为电热锅炉提供热能供应时需要的热负荷。

风能出力和负荷预测存在偏差，会对综合能源系统稳定运行造成一定影响。本文通过模糊变量对风能的计划功率和不同时间点的拟合负荷进行描述，因此综合能源系统需满足有功、备用限制条件，描述为

式中：Cr{·}为置信度函数；θDA为日前功率需符合的置信度条件；πDA为备用限制需符合的置信度条件；γDA为日前旋转备用因子；为慢机i相隔1min 的爬坡速度极大值；为快机i相隔1 min 的爬坡速度极大值；PWCur,t为时间点t的弃风容量；PRGi,t为慢机i的输出功率；uRGi,t为慢机i的调度状态；PFGi,t为快机i的输出功率；uFGi,t为快机i的调度状态；PILj,t为中断负荷j的参与容量[7]。

1.2.2 日内优化调度模型

相隔15 min 对综合能源系统进行一次日内优化调度，通过循环操作，实现全部时段的日内优化调度控制。

日内优化各阶段目标函数可描述为

式中：t0为日内调度控制的开始时间；Δt为执行周期；d为执行的周期总数；H5为机组启停状态改变产生的惩罚费用；Ii(t)为时间点t机组i的启停状态，取值为(0,1)；pi(t)为处于Ii(t)的惩罚成本；Py'cwt为日内优化调度阶段风电功率预测值；Pw't为实际调度值。

1.2.3 低碳调度求解

综合能源系统在购电、购气时的功率限制描述为

根据日前优化调度方案，设定各储能设备在24 h 内的容量不发生改变，描述为

式中：Soc(24)、Voc(24)、QH(24)分别为24 点时不同储能设备的容量；Socf、Vocf、QHf分别为Soc(24)、Voc(24)、QH(24)对应的容量初值。

综合能源系统实时优化阶段是在时间点t实现后一时间点各机组日内调度输出功率的修正，低碳调度优化求解结果为

式中：为风电机组实时功率预测值；为风电机组实时调度值。

日内、实时优化调度约束与日前优化调度相同，只对执行周期和调度运行间隔时间进行调整即可。

2 实验分析

以某一综合能源系统作为研究对象，系统采用分时电价策略，发电机容量为1 000 MW，发电量为5 000 万kW·h，碳排放因子为0.5 t CO2/（MW·h），碳排放费用为100 元/t。天然气购用单价为3.22元/m3，分别从日前、日内、实时3 个时间尺度对综合能源系统进行优化调度。

为了验证综合能源系统优化调度效果，设置3不同模式，对比分析不同模式下综合能源系统运行调度费用，结果如表1 所示。其中：模式1 在日前、日内、实时时间尺度中，风电预测偏差下降幅度分别为25%、12%、4%；模式2 在日前、日内、实时时间尺度中，风电预测偏差下降幅度分别为15%、8%、4%；模式3 在日前、日内、实时时间尺度中，风电预测偏差下降幅度分别为5%、4%、4%。

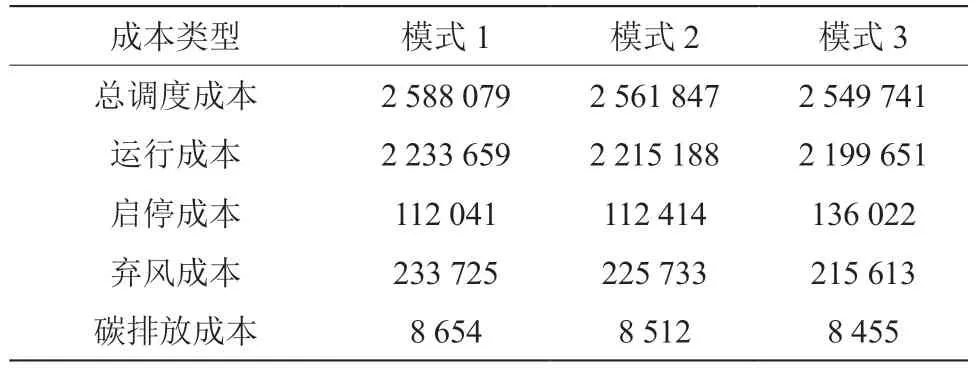
表1 不同模式的综合能源系统运行调度费用对比分析 单位：元

由表1 可知，当风电预测精度不断提升时，综合能源系统总调度成本随之减少，并可有效降低碳排放量。这是因为准确预测风电输出功率，可有效减小系统出力误差区间，从而大大降低了不确定性因素对综合能源系统的影响。实验结果表明，风电预测的不确定性对综合能源系统的优化调度具有直接影响，通过提高预测准确度能够达到优化调度成本的目标，但达到模式3 的预测条件后，继续追求准确性实现系统的优化调度难度较大，优化效果不再明显。

设定表1 中模式1 的条件为优化各阶段风电预测偏差，在优化调度的各阶段设定不同的负荷预测误差条件，对比分析不同条件下的系统调度费用。当用户响应与负荷预测间的误差为正值时，可有效提升风电利用率，并有效减小峰时段机组出力的边际成本，达到综合能源系统运行成本降低的目标。当误差为负时，则具有相反的优化效果。

将所提方法应用于综合能源系统的多时间尺度低碳调度优化，通过系统电、气、热负荷的优化控制结果分析所提方法的调度性能。结果显示：为实现综合能源系统最低运行成本目标，在电价低谷期将风力机组出力、电网购电作为主要方式；当电价处于高峰时段时，不再向电网购电来节省系统运行成本，启动储能设备配合微型燃气轮机、风力机组出力，以满足系统的用电需求。

3 结 论

以某一综合能源系统作为研究对象，将所提方法应用于系统的多时间尺度低碳优化调度，分析方法的有效性。实验结果表明：风电、负荷的准确预测，可降低综合能源系统的优化调度成本，并降低碳排放量。通过偏差预控机制降低源荷不确定性对系统不稳定的影响，可实现电、气、热负荷的优化调度，且预测结果与实际调度结果偏差不大。