周皓¹， 周晖²

(1.三峡大学职业技术学院，湖北 宜昌 443002；武汉大学电气工程学院，湖北 武汉 430072)

    摘 要：简述了电网无功电压综合控制的必要性，根据电力系统实际运行情况及SA算法自身的特点，就编码方式、状态产生函数、状态接收函数、初温、温度更新函数以及内、外循环终止准则等主要问题提出了改进SA算法。通过IEEE标准系统的仿真，说明改进SA算法具有搜索效率较高，原理及实现简单，速度快等优点。
    关键词：无功优化；模拟退火； 搜索策略

The improved SA algorithm in VAR and voltage control of power system

ZHOU Hao¹,ZHOU Hui²

(1.College of Technology,Three Gorges University,Yichang 443002,China;2.College of Electric Engineering,Wuan University,Wuhan 430072,China)

    Abstract: The necessity of VAR and voltage control in power system is simply introduced. A improved SA algorithm is proposed based on operational practice and the characteristic of SA, improvements are in aspects such as coding mode, the generator function, the accepting function, initial temperature, temperature updating function as well as the terminating condition of inner and outer cycle. The improved SA algorithm is proved to have higher efficiency, easy principle and realization, fast speed via the test in IEEE standard network.
    Key words: VAR optimizing Simulated annealing(SA) Search strategy

0  引言
    电力系统运行的一项重要任务就是为用户提供高质量的电能服务，维持电压在可接受的范围内。电力负荷每分每秒都在变化，电压会因负荷的改变而变化。此外，过多的无功功率在网络上传输将带来附加有功损耗，并造成电压波动。因此电力调度人员要控制各种设备，包括调节发电机电压，有载调压变压器分接头，投切静止补偿器和并联电容器，来实现跟踪负荷变化的动态电压和无功调节，以达到安全和经济的双重指标，这就是通常所说的无功电压综合控制问题。由于变压器变比和无功补偿装置容量的调节是离散的，因此它是一个混合整数、非线性规划问题。大量实用的规划技术，例如非线性规划法，二次规划法，线性规划法，线性规划和整数规划的混合算法及内点法，都被用于解决该问题，但实际效果都不理想。
    模拟退火(SA)算法是近年来逐渐兴起的一种启发式搜索法，已被引入到电力系统无功电压控制问题中，并取得了较为理想的效果^[1]。SA最早由Metropolis等人提出，它是一种基于Mente Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物体中固体物质的退火过程与一般组合优化问题之间的相似性^[2]。模拟退火算法的具有优化质量高、初值鲁棒性强、通用易实现的优点。相对于GA算法，它跳出局部最优的能力更强。但由于它是基于领域搜索的机制，因而为得到全局最优解，往往要花费较长的搜索时间。因此本文对SA算法进行了改进，并通过IEEE的数据进行了仿真，得到了较好的结果。

1  无功电压综合控制模型：
    电力系统无功电压综合控制是指满足系统各种运行约束的条件下，通过优化计算确定发电机的机端电压、有载调压变压器的分接头挡位和无功补偿设备投入等，以达到系统有功网损最小和各节点电压约束。其数学模型如下：
    目标函数：

有变压器和电容器动作次数的计数器；α ₁、α ₂、α ₃为各惩罚项的系数。
    等式约束：即为各节点有功和无功平衡约束。

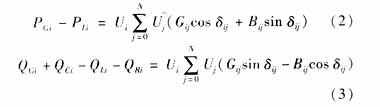
式中：N为 电网节点总数；P_Gi，P_Li为分别为节点i发电机有功出力和有功负荷；Q_Gi，Q_Ci，Q_Li，Q_Ri分别为节点i发电机无功出力、容性无功补偿容量、无功负荷和感性无功补偿容量；G_ij，B_ij，δ_ij分别为电网中节点i和j之间的电导、电纳和节点电压相角差。
    不等式约束：


2  改进SA算法：
    由于传统的SA算法为得到最优解，通常要求较高的初温、较慢的降温速率、较低的终止温度以及各温度下足够多次的采样，因而模拟退火算法往往优化过程较长，这也是SA算法最大的缺点。为加快收敛速度，提出改进SA算法如下：
2.1 编码方式
    编码就是将问题的解通过某种变换关系映射到某种数码空间，目的在于经过变换后的编码便于进行算法相应的各种操作。常用的编码方式包括十进制编码，二进制编码和实数编码。由于无功优化中有大量的控制变量且多为离散值，编码的好坏直接影响算法的执行效果。为了简化编码方式同时兼顾SA算子操作的方便性和效率，采用二进制编码，且各控制变量均按照各自的取值范围进行编码，即不同变量的编码可能具有不同的长度，如下图1所示。

由于不同设备在优化中具有不同的重要性(例如升高电压时应先投无功再调变压器分接头)，因此对不同设备可依据其重要性，对SA的各操作赋以不同的概率值，使作用大的控制变量有较多的机会得到进化。
2.2 状态产生函数
    即由原状态产生新状态的方式，通常是按照某一概率分布函数产生相应的随机变量，则新解由原解和该随机变量之和组成。为使搜索过程能尽可能的得到全局最优，产生的候选解应能遍布整个解空间。
    借鉴参考文献[4]中给出的随机变量产生函数以及对应的温度更新函数，本文拟采用下式来产生随机向量的第i个状态：

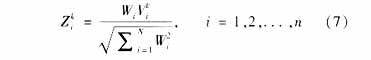
其中 W₁,W₂,^...,W_n是一组在［－1，1］上均匀分布的随机变量，n为设备总数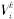，为具有概率密度函数g2(v |T_k)的随机变量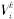，和g₂(· |T_k)分别由下两式给出：


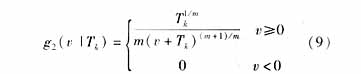
    其中 U₁,U₂,...,U_n是一组两两相互独立的在［0，1］上均匀分布的随机变量，v∈R，T>0，是给定参数，m≥1是给定的常数，T_k为对应的温度值。由于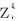的取值范围为(-∞,+∞)，因此还需将此随机变量归算到各设备的取值范围之内。则产生的新候选解为：

    式中H^k为新候选解，X^k为原始解，Z^k为产生的随机向量。此外，为了加速收敛，在温度较高时，只进行各设备二进制编码值向量中高位编码值的更新。这样可以在迭代初期只进行区域的搜索，减少为得到局部最优而浪费的时间。在迭代后期，则较多地进行各编码中低位值的更新，确保在小范围内搜索得到最优解，从而在提高搜索精度和加快搜索速度上达到平衡。
2.3 状态接收函数
    即在某一温度下，接受新解的概率。理论上，使目标函数值下降的候选解的接受概率应比使目标函数值上升的候选解的大；且随着温度的下降，退化解的接受概率要逐渐减少；当温度趋于零时，就只接收优化解。状态接收函数的引入是SA算法实现全局搜索的最关键因素，但其具体形式对算法性能的影响并不显著[1]，因此本文采用通常的做法，令

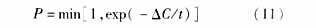
其中ΔC为旧个体与新个体的目标函数值之差。
2.4 初温
    理论上，初温应选择得充分大以使几乎所有产生的候选解都能被接受，以确保算法的全局收敛性。但初温越高，所需的计算时间越长。为综合考虑优化质量和优化效率，可先随机产生一组状态，以各状态目标值的方差为初温。 
2.5 温度更新函数
    在非时齐SA算法收敛性理论中，温度更新可采用函数t_k=α/log(k+k₀)，但温度下降很慢。而快速SA算法中更新函数取为t_k=β/(1+k)。但温度的下降必须与状态产生函数相匹配，才能保证算法可靠的收敛到全局最优。通常，各温度下产生候选解越多，温度下降的速度可以越快。为与状态产生函数相匹配，温度更新函数由如下指数退温函数定义：

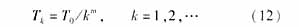
    式中T₀>0是初始温度，m≥1与(9)式定义的一维概率密度函数g₂(v |T_k)中的m相同。采用(7)式和(12)式定义的随机变量产生函数和温度更新函数可以得到较好的SA性能。
2.6 内循环终止准则
    又称Metropolis抽样稳定准则，用于确定在某一温度下，搜索是否已经收敛。常用的终止准则包括：(1)目标函数的均值是否已稳定；(2)最优目标函数值连续若干代不变化；(3)按确定的迭代步数。本文采用(2) ∪(3)的形式，在最大迭代步数内，最大目标函数值已收敛，则终止迭代，改变温度。若达到最大迭代步数仍未收敛也终止迭代。
2.7 外循环终止准则
    即算法终止准则。通常的做法包括：(1)设置终止温度值；(2)设置外循环最大迭代次数；(3)最优目标函数值连续若干步保持不变。本文采用(1)∪(3)的形式。若达到终止温度且最优目标函数值已稳定，则优化结束；否则，可适当提高温度，继续搜索直至最优解达到稳定状态。
    此外，为了不漏掉搜索过程中产生的最优解，将"best so far"状态记录下来；根据实际要求，灵活处理终止准则，即速度优先的情况下，可适当放宽收敛条件；而质量优先时，则可多次提升温度，反复寻优，尽可能得到全局最优解。

3  算法流程
    由上述部分所介绍的改进SA算法，其流程如下图2所示：

4  算例及分析
    基于改进SA算法的无功优化程序在IEEE30节点的系统中进行了计算，IEEE30节点网络包含6个发电机节点、22个负荷节点和41条支路。各无功调节设备的调节范围如表1所示。改进SA算法与简单遗传算法(SGA)及其它文献中的方法进行了比较，结果如下表2所示：

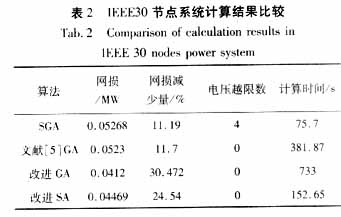
    由计算结果可见，较之SGA算法，及改进GA算法，改进SA算法在较短的时间内更有效地降低了网损，减少了电压越界节点数，优化了整个系统的电压水平和电压分布，同时也较好的控制了计算时间。

5  结论
    (1)改进SA算法原理简单，且操作方便易行；
    (2)由于采用了适当的随机变量产生函数，能保证搜索在整个解空间中进行，从而确保了得到最优解的概率；
    (3)通过惩罚项来实现约束条件，简化了处理过程，同时也可避免当最优解必须经过非可行解来过渡时，无法达到最优的情况；
    (4)由于在不同进化阶段采取不同的策略，缩短了区域搜索的时间，减少了花在优化效果差的设备编码上的时间，从而提高了优化效率；
    (5)由于仍为邻域搜索，计算时间依然偏长，可考虑整合一些并行搜索策略并采用专家系统来构造初始解，来缩短进化进程。

参考文献

[1] 顾丹珍，徐瑞德.一种地区电网多目标无功优化的新方法——改进模拟退火算法.电网技术.1998，22(1).
[2] 王凌.智能优化算法及其应用.北京：清华大学出版社，施普林格出版社，2001.
[3]Yutian Liu,Li Ma,Jianjun Zhang,"GA/SA/TS Hybird Algorithms for Reactive Power Optimization",IEEE Tran. On Power Systems,January 2000:245-249.
[4] 杨若黎，顾基发.一种高效的模拟退火全局优化算法.系统工程理论与实践.1997，第五期.
[5]赵登福，周文华，张伏生等.遗传算法在无功优化应用中的改进.电网技术.1998，22(10).