周 浩1, 陈建华1, 韩祯祥1, 王冬明2, 孙维真2
(1.浙江大学电气工程学院, 杭州 310027;
2.浙江省电力调度通信中心, 杭州 310007)
摘 要: 利用平均电价差值积分模型将电力市场中发电商的机组报价曲线转换为一维特征向量，从而采用传统聚类方法对机组报价曲线实现分类。通过对某电力市场的报价曲线聚类计算表明，在平均电价差值积分模型中使用20段分段模型，并采用离差平方和法进行聚类，可以对电力市场中机组的报价曲线实现较准确有效地分类。还可以采用量价指数CPI、HHI指数等方法对 聚类结果进行进一步分析。
关键词: 电力市场; 报价曲线; 离差平方和法; 聚类分析; HHI指数; 量价指数
Cluster Analysis of Power Producer's Bidding in Electricity Market
ZHOUHao1, CHEN Jianhua1, HANZhenxiang1,WANG Dongming2, SUN Weizhen2
(1.College of Electrical Engineering of Zhejiang University,
Hangzhou 310027, China；
2.Zhejiang Power Dispatching & Communications Center, Hangzhou 310007, China)
Abstract: An average electricity price differenceintegration model is proposed in this paper.This model can transform unit's bidding curve of power producer in market into a onedimensional feature vector,so it canimplement classification of unit's bidding using classical clustering method.Through clustering calculation of bidding curve from certain electricity market,it is shown that bidding curve can be classified accurately and efficiently using 20segment model and square sum of deviations in the average electricity price differenceintegration model.Moreover,CPI (Capacity Price Index),HHIindex can be used to analyze the bidding clustering results further.
Keywords: electricity market; bidding curve; square sum of deviations; cluster analysis; HHI; capacity price index
1引言
发电商对电力市场具有重要影响，因此对发电商的报价进行计算分析和分类研究是十分必要的。一般情况下，电力市场中竞价上网的发电商个数不会太多，容易形成事实上的寡头垄断，所以有关发电商报价策略方面的研究显得尤为重要。文献［1~10］采用博弈论、遗传算法和蒙特卡罗方法等多种算法对发电商的报价策略进行了理论分析和计算，但这些方法侧重于对个体电厂进行报价策略指导，通常是一种事前分析，无法胜任电力市场中对所有电厂报价的宏观分类和整体分析。实际上从电力市场监管的角度出发，对所有电厂报价进行整体分类分析具有更大的意义。
将电厂报价进行分类，使电力市场的运行管理部门和监管部门借助电厂报价的分类，采用更细化的定量指标或分析手段进行更具体地量化研究，以监控和监管各种不同报价情况对电力市场的影响，对电力市场的安全稳定运行具有十分重要的意义。截止目前有关电厂报价的分类研究的工作开展得很少，本文主要采用聚类分析的方法进行了研究。然后进一步采用量价指数CPI和HHI指数等方法对报价分类结果进行更具体的研究。
聚类分析是工程上较多采用的分类方法，但是传统聚类分析方法［11，12］无法直接 应用于报价分析，主要是由于电力市场中机组报价是一组分段递增的报价曲线，而传统聚类分析方法只能对多维空间中的点集进行分类，无法对一组曲线进行分类。本文提出了平均电价差值积分模型，先对上网电价报价曲线进行数据转换，再采用聚类分析方法对机组报价进行分类。采用该方法对某电力市场2002年第三季度的报价数据进行了聚类分析，其结果表明，采用平均电价差值积分模型对报价曲线进行数据转换，可以较好地解决电力市场中报价曲线的分类问题，该方法对发电商的报价进行分类研究是可行的。
2平均电价差值积分模型
聚类分析是数理统计分析中研究“物以类聚”的一种方法。它是将一批样品或变量，按照它们性质上的亲疏程度进行分类。通常有两种方法：一种是把每个样品看成是p维空间的一个点，在p维坐标中，定义点与点之间的某种距离；另一种是用相似系数来描述点与点的亲疏程度，在确定样品或变量的相似系数或距离后，可对样品或变量进行分类。
在某电力市场中，某一时段各发电商的报价数据是2×10维（每个机组分十段报价，每段报价包括段电价和段容量两个变量），整个电力市场的报价数据为R×2×10维（R为参与竞价的发电商数目）。显然，传统聚类方法中的方法1或方法2，都无法直接应用于电力市场报价 曲线的分类，为此采用下面方法对发电商报价曲线进行数据转换。
2.1报价曲线的分段量化
首先将报价曲线标么化，机组的报价容量以机组可用容量为基准，电价以电力市场价格上限 为基准。只有进行标么化，不同容量机组的报价之间才有可比性。
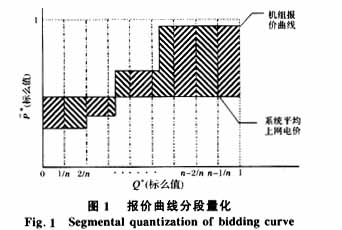
然后将各发电商的报价曲线分段量化，如图1所示。把报价曲线容量均匀分成n（n可取10，20，50等）段，用Q*来表示；各段电价标么值用P*来表示；系统年平均上网电价标么值用P*来表示。故有
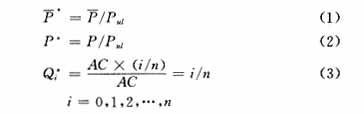
其中：
为电网年（或上一年）平均上网电价（元/(MW·h)）；
P为机组报价的各段电价（元/(MW·h)）；
Pul为电力市场的价格上限 (元/(MW·h))；
AC为机组可用容量；
n为报价容量的分段数。
2.2进行平均电价差值积分得到机组报价曲线的表征向量
（1）某一时段i的机组报价曲线表征向量
定义差值积分如下：
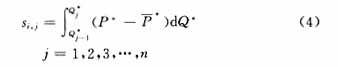
其中：i表示第i时段；j表示报价曲线分段量化后的第j段。
由此，图1中的阶梯状报价曲线可转化为离散的1×n维数组。显然增大该数组的维数n（分段数），可以更加有效地反映原报价曲线与平均上网电价之间的关系，用Si来表示：
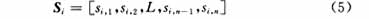
因此，可以用向量Si来表征第i时段的某机组报价曲线。
（2）一天48个时段（某一天Day）的机组报价曲线表征向量
该电力市场以每半小时为一个时段，全天共分48个时段。对某天48个时段的每个时段进行差值积分处理，可得
显然，LD较好地反映一天中报价曲线偏离平均电价的变化，可以用来表 示一天中上网电价报价曲线的变化。
（3）某一段时间（1周、一月、一季度、半年、一年等）的机组报价曲线表征向量
将一段时间内每天的LD值进行平均，即可得到一段时段内的相关报价平均值，用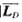
来表示：
m—统计时间段内的总天数；
lk,i—表示第k天第i时段的报价曲线表征向量。
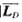可以较好地反映一段时间内平均报价曲线偏离平均上网电价的变化，可用来表示一段时间内上网电价报价曲线的变化。
3聚类分析方法
采用上一节平均电价差值积分模型，可以得到较好地表征机组报价曲线的向量Si、LD或LD，它实际上代表了某一n维空间中的一点，因此可以采用系统聚类法进行分类。报价曲线分类中采用何种聚类方法较好，报价曲线分段量化以多少段为宜，这是本节重点讨论的问题。
3.1确定聚类分析方法
对报价曲线采用平均电价差值积分模型进行数据转换后，再进一步采用系统聚类法对发电商报价进行聚类分析。
系统聚类法是把个体逐个地合并成一些子集，直至整个总体都在一个集合之内为止。它是聚类分析中应用最广泛的一种，凡是具有数值特征的变量或样品都可以采用该方法进行分类。对发电商报价进行聚类分析的步骤如下：(1)聚类前先对数据进行变换处理，得到表征报价曲线的特征向量。(2)聚类分析处理开始时，先将各样品自成一类，计算各样品之间的距离，再将距离最近的两个样品并成一类。(3)选择并计算类与类之间的距离，继续合并直至样品归为一类为止。(4)绘制系统聚类谱系图，按不同的分类标准或分类原则，得出不同的分类结果。在(2)中根据类间距离计算的不同，可以得到多种不同的聚类分析方法：最短距离、最大距离、平均距离、重心距离、离差平方和等。纵观这几种方法在不同领域中的分类应用效果，通常以离差平方和法的分类效果较好，故选择离差平方和法进行分类计算。
离差平方和法的分析是：如果类分得合理，则同类样品之间离差平方和应该较小，类与类之间的离差平方和应该较大。经过上述系统聚类法处理后，得到聚类树状谱系图。借助于该图，可以直观地将研究对象亲疏关系反映出来。
采用离差平方和法，选取2002年8月14日该电力市场的报价数据进行聚类分析，其中报价曲线分段数取20，电力市场价格上限取820元/(MW·h)，聚类计算的分析结果如图2所示。
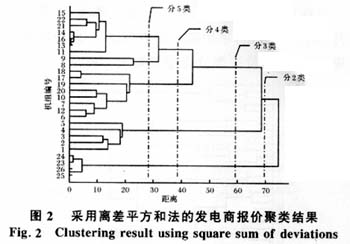
结合实际报价数据并参照图2的聚类结果，可以发现将聚类结果分4类与实际报价情况比较吻合。其中8号发电厂4台机组的报价最高，归为一类；1号发电厂5台机组报价较高，归为一类；3号发电厂2台机组及其他报价次高机组归为一类；其他报价普遍较低的机组归为一类 。
3.2确定报价分段数目
理论上，报价曲线分段数越多，越能真实地反映原报价曲线，但是分段数过多会造成计算量大大增加，报价曲线分段数究竟以多少段为合适是一个需要进行研究的问题。为此，选取与图2完全相同的报价数据，但将分段数由20增加至50，再进行聚类分析（类间距离计算采用离差平方和），分析结果如图3所示。
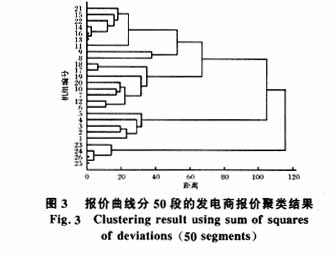
比较图2与图3，分段数增加仅仅改变了一些很小的分类细节，重要大类并没有发生实质性的变化，但是当分段数从20段增加到50段之后，不论计算时间还是计算强度都增加很多，因此将报价曲线分成20段已能较真实地反映报价曲线的变化。建议在对机组报价进行聚类分析时采用20段分段。
4聚类计算结果及其分析
选用该电力市场2002年第三季度（7月-9月）的报价数据，采用离差平方和法20段分段进行聚类分析，报价聚类分析结果如图4所示。
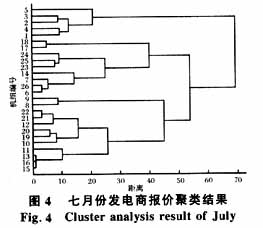
7月份实际报价情况，主要是1号发电厂的机组报价较高。聚类计算结果将报价较高的1号发电厂机组聚为一类，而将报价较低的其他电厂机组聚为另一类，聚类分析计算结果与实际情况是比较吻合的。下面采用量价指数、HHI指数进行更具体的分析。
4.1量价指数分析
4.1.1量价指数CPI（Capacity Price Index）定义
量价指数CPI是作者为进行电力市场报价分析而定义的一个指标，它可以较好地反映电厂报价中的高报价行为［13］，具体定义如下：
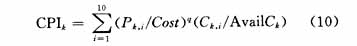
式中：CPIk表示k机组在某时段的量价指数；Pk,i表示k机组在相应时段报价的第i段价格；Cost表示系统平均发电成本；q是幂指数，可以取2~5，通常取3；Ck,i表示k机组在相应时段报价的第i段容量，与Pk,i一一对应；AvailCk表示k机组在相应时段的可用容量。
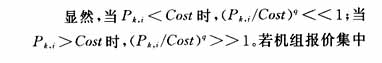
在高价段，则其量价指数将比正常机组报价的量价指数高出许多，可以突出反映高价位的容量段。
式中的段价格、段容量都已经转换为相对值，因此，将某一时段属于同一电厂的所有机组的CPI取平均值，得到对应该时段的该电厂的CPI值；又进一步将电力市场中的所有机组的CPI取平均值，得到对应该时段整个系统的CPI值；再将全天48个时段的CPI取平均值，得到某机组或整个系统当天的CPI值。依此类推就可以得到各月、各季、半年、全年以及某一个任意时段的CPI值。
4.1.2聚类结果的CPI分析
对聚类分析得到的两类电厂报价分别计算CPI值，如表1所示。
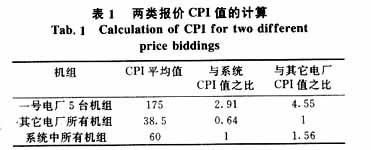
显然，1号电厂5台机组的CPI值远远高于其它电厂机组，为电力市场全系统平均值 的近3倍，为其它电厂机组CPI值的4.55倍。充分反映了1号电厂5台机组同时采用了高报价策略，对于供电十分紧张的7月份来说，会使电价产生较明显的升高。统计表明，该月中超过12%的时段电价处于涨停位置（价格上限），全月的平均电价超过322元/(MW·h) 。
4.2HHI指数分析
HHI指数是经常用来评估市场力的指标，下面采用它们对聚类分类结果进行进一步的分析。
由于1号电厂的5台机组采用了基本相同的报价模式，可以看作是一台大机组，占市场竞价机组总容量的45%，市场份额太大，显然，此时若采用HHI指数进行计算，它的HHI值就可达2025（尚未考虑其它机组对HHI指数的影响），已明显超过1800的限值（美国评判标准），呈现出很强的市场力。因此，在夏天电力负荷高峰时期，该电厂的报价对市场电价具有决定性的影响。
综上所述，由聚类分析结果结合CPI、Lerner指数和HHI指数的分析，可以发现7月份该电力市场存在较强的市场力,并对电价产生影响。
5结论
电力市场中对发电商的报价进行聚类分析，使监管机构能准确及时地掌握各种异常报价行为，以保证电力市场安全稳定地运行。
根据上述分析，可以得到以下结论：
(1)采用平均电价差值积分模型，可以有效地将报价曲线转换成能较好反映报价曲线变化的一维特征向量，从而对机组报价曲线实现比较准确有效的分类。
(2)对报价曲线实施过多的分段会大大增加计算量和计算时间，但对分类结果没有太大的影响。在通常的情况下，报价曲线以分20段为宜。
(3)在各种聚类分析法中，以离差平方和法的聚类分析结果最好，与实际机组的报价情况比较吻合。
(4)将平均电价差值积分模型和离差平方和法结合，可以对电力市场中的机组报价实施较准确有效的分类。
本文对一组曲线实行聚类分析的方法，对解决其他领域的类似问题具有较好的借鉴意义。
(5)采用平均电价差值积分模型对电厂报价进行聚类分析后，可以进一步采用量价指数CPI、HHI指数等方法对上述结果进行进一步地具体分析。
参考文献
［1］Hos S．A study of basic strategy in clearing pricingauction［A］．In：Proceedings of the 1999 IEEE PESPower Industry Computer Applications Conference（PICA＇99）［C］．Santa Clara（CA）：1999．55－60
［2］Zhang D Y，Wang Y J，Luh P B．Optimization basedbidding strateries in the deregulated market［A］．In：Proceedings of the 1999 IEEE PESPower IndustryComputer Applications Conference（PICA＇99）［C］．Santa Clara（CA）：1999．63－68
［3］Mielczarski W，Mlchalik G，Widjajrrj M．Bidding
strategies in electricity markets［A］．In：Proceedingof the 1999 IEEE PES Power Industry ComputerApplications Conference（PICA＇99）［C］．Santa Clara（CA）：1999．71－76
［4］Wen F S，David A K．Optimalbidding strategies andmodelling of imperfect information among competiti－ve generators［J］．IEEE Trans on Power Systems，2001，16（1）：15－21
［5］Ritchter Charles W，Sheble Gerald B．Comprehensivebidding strategies with genetic programming［J］．IEEE Trans on Power Systems，1997，12（4）：1207－1212
［6］Li Chao－an，Svoboda Alva J．Revenue adequatebidding strategiesin competitive electricity markets［J］．IEEE Trans on Power Systems，1999，14（2）：492－497
［7］Ferrero R W，Rivera JF．Application of games withincomplete information for pricing electricity inderegulated power pools［J］．IEEE Trans on PowerSystems，1998，13（1）：184－189
［8］Ferrero R W，Shahidehpour S M，Ramesh V C．Transaction analysis in deregulated power systemsusing games theory［J］．IEEE Trans on Power Systems，1997，12（3）：1340－1347
［9］张宇波，罗先觉，薛钧义．非完全信息下电力市场中电厂机组竞价上网的博弈解［J］．电力系统及其自动化学报，2003，15（1）：27－32
［10］马莉，文福拴，David A K．采用分段报价规则的竞价策略初探［J］．电力系统自动化，2001，25（19）：16－19
［11］Bow Sing－Tze．Pattern Recognition，Application toLarge Dataset Problems［M］．1984
［12］边肇祺．模式识别［M］．北京：清华大学出版社．1988
［13］周浩，陈建华．量价指数及其在电力市场报价分析中的应用［Z］（待发表）．
附录A：
