摘要：通过对常见的阻容耦合、变压器耦合及直接耦合方式下共发射极放大电路交流负载线特性的研究，给出了三种耦合方式下放大电路交流负载线的共同形式，以及常见三种耦合方式下共发射极放大电路交流负载线的具体形式，阐述了这三种耦合方式下放大电路交流负载线的相同和不同之处，以及三种耦合方式直流负载线方程与交流负载线方程的关系。

0 引言

图解法在用于放大电路分析时，由于其形象直观而常用于放大电路静态工作点及波形失真问题的分析。其中，交流负载线则用于估算最大不失真输出电压。但是，目前高等院校电子线路教材并没有给出交流负载线方程的形式及其推导过程，只给出交流负载线的斜率和画法。因此，在一些文献中采用戴维南定理或叠加定理等方法推导和讨论了共射极阻容耦合放大电路或直接耦合放大电路的交流负载线方程，但是对变压器耦合放大电路并未作推导和讨论。

本文对反映放大电路输出特性的阻容耦合、变压器耦合以及直接耦合方式下共发射极接法放大电路的交流负载线进行了分析和研究，给出了这三种耦合方式下共发射极放大电路交流负载线的特性，并对变压器耦合放大电路的交流负载线方程进行了推导。

1 交流负载线及其方程形式

放大电路在交流信号源和直流信号电源共同作用时，晶体管管压降△uce和集电极电流△ic通过交流等效负载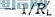所表现出的关系△ic=f(△uce)描述了交流信号输入后动态工作点移动的轨迹，这一直线我们将其称之为交流负载线。

由文献知，阻容耦合、变压器耦合及直接耦合方式共射极放大电路的交流通路输出端均为如图1所示的形式。其输出端交流电压、电流关系为：

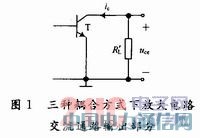
对阻容耦合及直接耦合而言，集电极负载是Rc和RL的并联值，即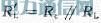。对变压器耦合而言，集电极负载是，n为变压器变比。

将交流量、直流量和总的瞬时量之间的关系△ic=Ic+ic，△uce=Uce+uce代入式(1)得：

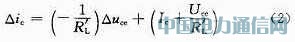
式(2)代表了通过Q点，斜率为的直线，即为放大电路交流负载线方程。该方程在纵轴上的截距为，在横轴上的截距为。若设，则其在纵轴和横轴上的截距也可分别表示为，这与直流负载线在纵轴和横轴上的截距表现形式完全相同。

2 三种耦合方式下交流负载线的特点、

2．1 阻容耦合放大电路

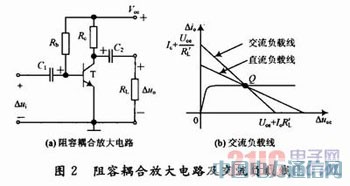
阻容耦和共射极放大电路及交流通路的输出部分如图2(a)，图2(b)所示，其直流负载线方程为：

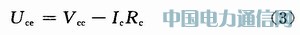
其输出端交流电压、电流关系如式(1)所示。整理式(3)和式(1)得交流负载线方程，如式(2)所示。

由式(3)和式(2)可画出直流负载线和交流负载线，如图2(b)所示。从图中可看出，直接耦合放大电路的直流负载线和交流负载线的斜率不同，交流负载线更陡。

2．2 直接耦合放大电路

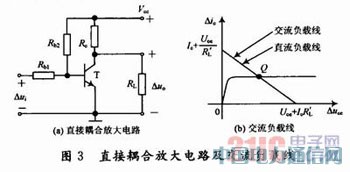
直接耦和共射极放大电路及交流通路的输出部分如图3(a)及图1所示，其直流负载线方程为：

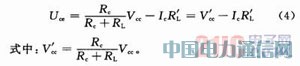
其输出端交流电压、电流关系如式(1)所示。整理式(4)和式(1)得交流负载线方程，如式(2)所示。

由式(4)和式(2)可画出其直流负载线和交流负载线，如图3(b)所示。从图中可看出，直接耦合放大电路的直流负载线和交流负载线重和，斜率相同。

2．3 变压器耦合放大电路

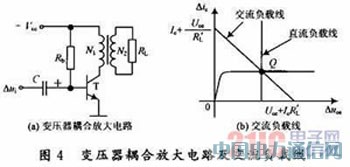
变压器耦和共射极放大电路及交流通路的输出部分如图4(a)及图1所示。忽略变压器初级线圈内阻，其直流负载线方程为：

其输出端交流电压、电流关系如式(1)所示。整理式(5)和式(1)得交流负载线方程，如式(2)所示。

由式(5)和式(2)可画出其直流负载线和交流负载线，如图4(b)所示。从图中可看出，变压器耦合放大电路的直流负载线和交流负载线的斜率不同，直流负载线更陡，是一条几乎垂直于横轴的直线。

3 结语

从真正意义上讲，所谓交流负载线方程应为式(1)，但该式在△ic-△uce平面内是一条过原点的直线，不能反映放大电路动态量与静态量相叠加及输入交流信号后动态工作点移动的真正轨迹，所以称式(2)为放大电路的交流负载线方程。不过可将式(2)理解为式(1)原点对应Q点后得到的方程，即式(2)为式(1)与放大电路直流负载线方程相叠加的结果。总之：

(1)三种耦合方式的放大电路交流负载线方程形式是相同的，斜率均为，方程在纵轴上的截距为，在横轴上的截距为，且通过静态工作点。另外，在纵轴和横轴上的截距表现形式与直流负载线相同。

(2)由于耦合方式及电路形式的不同，三种耦合方式放大电路的交流负载线与其直流负载线斜率相比，表现出了不同的特性，反映出不同的耦合方式对放大电路动态性能的影响。

(3)三种耦合方式的放大电路交流负载线方程均可由式(1)及其直流负载线方程相叠加而得出，反映了放大电路中瞬时量为交流量与直流量相叠加的特点及交流量是“驮载”在直流量上的特性。

(4)由静态工作点的高低很容易得知，放大电路是截止失真还是饱和失真，以此可调整静态工作点来消除失真。另外，根据交流负载线方程，比较Uces-Uce和，取较小者即为放大电路的最大不失真输出电压幅值。