椭圆球面波函数(Prolate Spheroidal Wave FunctiON，PSWF) 脉冲具有最佳时域能量*性和频谱灵活可控性的特点，被认为是符合超宽带(ultra-wideband，UWB) 系统要求的一种性能优良的脉冲。首先给出了满足FCC频谱掩膜要求的UWB脉冲波形设计方法，并将该方法应用于多进制TH PPM超宽带系统中。分析了多进制TH PPM超宽带系统原理，理论上推导了基于PSWF脉冲的多进制PPM-UWB系统的符号差错率公式，并与高斯脉冲进行比较。仿真结果表明，基于PSWF脉冲的UWB系统符号差错率性能要明显优于Gauss脉冲。

0 引言

UWB技术具有抗多径干扰、数据传输速率高、发射信号功率谱密度低和隐蔽性好等特点，目前在短距离无线通信系统中得到广泛应用。脉冲波形设计技术是超宽带通信中的关键技术之一。超宽带系统中脉冲波形应满足FCC频谱掩膜条件，并与窄带系统有较好的共存性。PSWF由于具有高能量*性、双正交特性和频谱可控性，并可以根据频谱模板的要求自适应地设计波形，因而被认为是符合UWB通信系统要求的一种性能较理想的脉冲。提高信息传输的可靠性和有效性始终是所有通信系统所追求的目标，误码性能是衡量一个通信系统可靠性的主要指标。在满足FCC频谱掩膜的前提下，将PSWF脉冲应用于多进制TH-PPM超宽带系统中，并对该系统的抗噪声和多址干扰性能进行分析和研究，得到了符号差错率(symbol error ratio，SER) 的解析表达式，进行了计算机仿真。

1 基于PSWF的UWB脉冲设计

Slepian和Pollack在文献[4]中首次提出，频域带限且持续时间为一个码元的时域能量*性最佳的信号形式是椭圆球面波函数。PSWF作为一种UWB脉冲，在波形设计层面上为解决系统干扰和实现频谱兼容提供了一种新的途径，因而被认为是符合UWB系统要求的一种性能较理想的脉冲。用φ n(c，t)表示n阶PSWF，其中，c=TsΩ，φ n(c，t) ∈【Ts/2，Ts/2】，Ω为函数的带宽。PSWF函数的积分方程定义如下式：

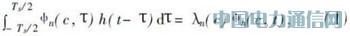
式中，λn(c)为该方程的特征值。

PSWF作为一种正交函数，与其他正交函数不同的是，PSWF不仅是时间的函数，同时还受时频联合参数c的控制。利用PSWF的这一特性，通过调整该脉冲函数的参数来实现脉冲的频谱搬移和带宽控制。FCC频谱掩膜要求如图1所示，其中实线和虚线分别为室内和室外频谱模板。将频谱掩膜等效为一个理想带通滤波器，其上限和下限截止频率分别为10.6GHz和3.1GHz。该理想带通滤波器的冲激响应h(t)为

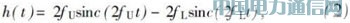
式中，fU=10.6GHz，fL=3.1GHz。将式(2) 代入式(1) ，并用文献[5]中的Parr算法求解该方程得到φ (t)即为PSWF脉冲，该脉冲的功率谱密度如图1所示。由图1可见，该脉冲能较好地满足FCC频谱掩膜的要求。

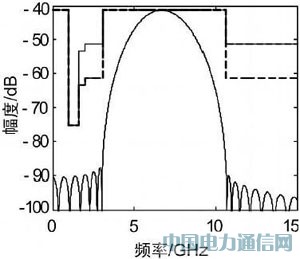
图1 基于PSWF的UWB脉冲频谱图