摘要：通过对常用快速傅里叶变换算法原理的研究分析，提出了一种简单有效的FFT算法实现方案，该方案已经在TMS320C64x DSP中实现。将FFT算法程序在CCS3.3中运行，验证了该方案的可行性、高效性。该方案已应用于LTE—TDD无线综合测试仪表的开发中。

在数字信号处理中，离散傅里叶变换(DFT)是常用的变换方法，它在各种数字信号处理系统中扮演着重要的角色。快速傅里叶变换(FFT)[1-2]是离散傅里叶变换的快速算法，它是根据离散傅里叶变换的奇、偶、虚、实等特性，对离散傅里叶变换的算法进行改进获得的，两者都是为了将信号变换到频域并进行相应的频谱分析。对于实时性要求很强的信号处理来说，运算速度对整个处理的影响是显而易见的。因为FFT拥有很高的运算能力，使其在无线通信和数字通信、高速图像处理、匹配滤波等领域得到极为广泛的应用。

LTE作为准4G技术，以正交频分复用OFDM和多输入多输出MIMO技术为基础，下行采用正交频分多址(OFDM)技术，上行采用单载波频分多址(SC-FDMA)技术，在20MHz频谱带宽下能够提供下行100Mb/s和上行50Mb/s的峰值速率[3]。

频域分析比时域分析更优越，不仅简单，且易于分析复杂信号[4]。在LTE系统中，FFT算法主要应用于基带信号生成、信号的接收和检测等，将时域信号转移到频域进行处理。

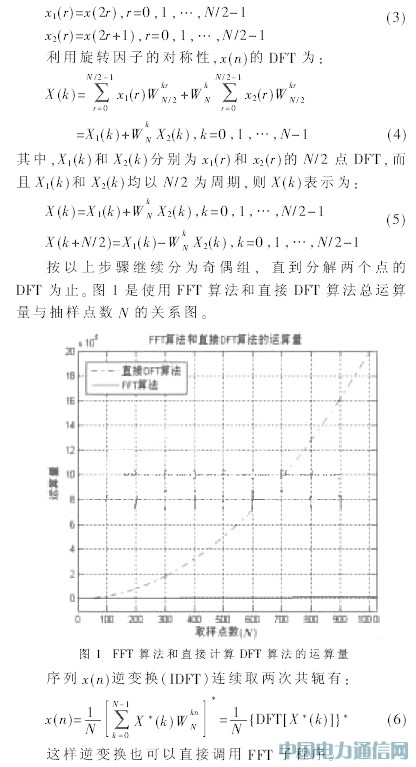
其中，x(n)为复数序列，WNkn和X(K)也为复数，因此每计算一个X(K)值，需要进行N次复数乘法运算和N-1次复数加法运算。而X(K)共有N个点，所以完成整个DFT运算需要进行N2次复数乘法和N(N-1)次复数加法运算，当N很大时，运算量相当可观。然而对于实时性很强的信号处理来说，如满足其要求，运算速度就太高了。利用旋转因子WNkn的对称性、周期性和可约性，可以使DFT运算中的有些项合并，将长序列的DFT分解为几个短序列的DFT，从而大大减少运算次数。FFT算法可以分为时间抽取法和频域抽取法两大类。频域抽取法的运算特点与时间抽取法的基本相同，不同之处是频域抽取法的蝶形运算是先加后乘，时间抽取法的蝶形运算是先乘后加；频域抽取的输入序列是自然顺序，输出序列是倒序，而时间抽取法的输入序列是倒序，输出序列是自然顺序。

假设输入序列x(n)长度为N=2M，M是正整数。如果不满足这个条件，在序列尾部人为地加上若干零值点，使其达到这一要求。将序列x(n)按n的奇偶分解为两个N/2点的子序列：

2 FFT算法的DSP实现

2.1 硬件

TMS320C6000系列DSP是TI公司推向市场的高性能DSP，综合了目前性价比高、功耗低等优点。TMS320C64系列提高了时钟频率，在体系结构上采用了VelociTI甚长指令集VLIW(Very Long Instruction Word)结构[5]，芯片内有8个独立功能单元的内核，每个周期可以并行执行8条32bit指令，最大峰值速度为4800MIPS，2组共64个32bit通用寄存器，32bit寻址范围，支持8/16/32/40 bit的数据访问，芯片内集成大容量SRAM，最大可达8Mb。由于出色的运算能力、高效的指令集、大范围的寻址能力，使其特别适用于无线基站、测试仪表等对运算能力和存储量要求高的应用场合。

2.2 FFT算法的DSP实现

FFT算法作为一个子函数模块且输入序列长度不尽相同，所以，方案定义了输入输出变量及其调用格式。调用格式：Turbo_Code(int*，int，int，char*，char*，int*)，其中，int分别表示输入序列的长度和FFT的级数；int*分别表示输入序列的首地址和输出序列的首地址；char*分别表示旋转因子的余弦的首地址和旋转因子的正弦的首地址。

FFT算法具体实现流程如下：

(1)时间抽取法的FFT中，每个蝶形的输入、输出数据节点在一条水平线上，所以每个蝶形的输出数据可以立即存入原输入数据所占用的存储单元。这种原位计算可节省大量的内存，并且理论上减少不同寄存器之间存取数据的时间。

使用C语言编写主函数，汇编语言编写FFT算法的实现函数。程序中假设输入数据最大长度为1024，由于DSP C6455可以直接存取处理32bit，所以在内存中定义了长度为8192bit作为存放输出序列的内存空间。为了提高运算精确度，输入数的实部和虚部分别占用一个字，在程序中进行复数相乘操作是采用汇编指令MPYHI。内存定义了长度为2048bit的Tempsequence作为存放倒序序列，并且建立了2张旋转因子查找表，分别为Wr和Wi。

外循环中，在每次内循环之前从输入比特序列中取出32bit放入一个寄存器，作为一个内循环的输入，内循环结束后，取下一个32bit输入比特更新这个寄存器。

内循环中，计算蝶形过程采用查表的方式。对于每一级，计算出需要的旋转因子个数以及相同旋转因子相距的间隔。计算蝶形过程时，首先提取出X(k)，根据相同旋转因子间隔找到X(k+B)完成蝶形计算。考虑到旋转因子的对称性，在内存中存放旋转因子时只存放一半，剩余的数据根据对称性进行处理。图2给出了FFT算法实现计算流程图。

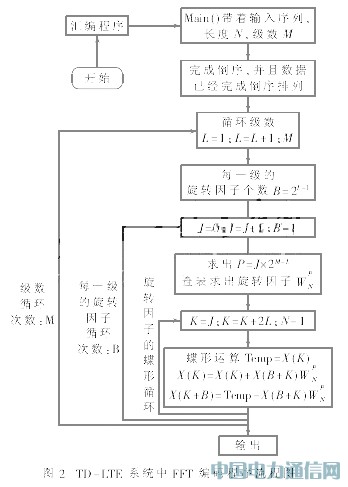
按时间抽取法的FFT输入序列是倒序，输出序列是自然顺序；按频率抽取法的FFT输入序列是自然顺序，输出序列是倒序的。不管采用哪种方法进行FFT计算，都需要倒序处理。倒序是整个FFT计算的重要部分，进行汇编程序时，按自然顺序将输入数据存入到存储单元内，通过变址运算，将自然顺序的序列按时间抽取法要求进行倒位。

重新排序之前，存储单元Y中依次存放输入数据，I表示当前输入数据比特的顺序数的十进制数值，I的取值从0到N-I；J表示当前倒序数的十进制数值。输入序列的第一个和最后一个数的位置不需要倒序处理，完成倒序的外循环的次数为N-2。为了保证调换数据的正确性，需要检测一下是否I<J，只有当I<J，才将Y(I)与Y(J)的内容互换。形成倒序数J以后，就可以实现变址功能，按照自然顺序存放在存储单元的数据重新按照倒序排列。图3给出了实现倒序的汇编流程图。

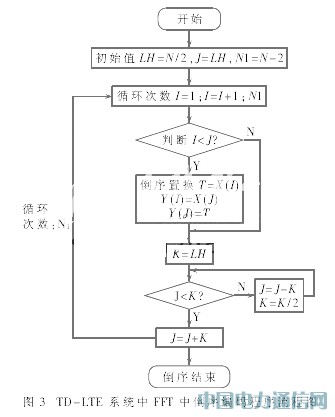
3 性能分析与总结

在DSP软件实现中，通过指令并行，尽量优化程序循环体，减少或消除程序中的’NOP’指令[6]。通过程序仿真运行，得到统计结果如表1所示。

从表中可以看出，当运用TMS320C64×DSP芯片实现时，由于处理器的超高主频一般为1GHz，一个指令周期耗时为1ns，其运算速率非常快，完全可以满足实时性信号处理。因此，采用旋转因子查表法的实现方案不仅简化了程序实现方法，还减少了模块程序代码编写，节约了系统存储空间。

本文提出了一种简单有效的FFT算法实现方案，详细介绍了算法在DSP的实现方法，并在TMS320C64x芯片上加以实现。程序运行结果表明，该算法能够满足TD-LTE系统的需求，具有可行性和高效性。该方案已应用于LTE-TDD无线综合测试仪表的开发中。

参考文献

[1] 丁玉美.数字信号处理[M].西安：西安电子科技大学出版社，2002.
     [2] 何方白，张德民.数字信号处理[M].北京：高等教育出版社，2009.
     [3] 3GPP TS 36.211 v9.0.0.Evolved universal terrestrial radio access(E-UTRA) physical channels and modulation (Release 9)[S].2009-12.
     [4] SAIDI A.Decimation-in-time-frequency FFT algorithm[M]. Manuscript，To be published.1993.
     [5] Texas Instruments Incorporated.TMS320C64x/C64x+DSP CPU and instruction set referenceguide[EB/OL].Http://www.ti.com.cn，2008.
     [6] Texas Instruments Incorporated.TMS320C6000系列DSP编程工具与指南[M].田黎育，何佩琨，朱梦宇，译.北京：清华大学出版社，2006.