摘要：介绍了差分跳频技术的基本原理，分析了差分跳频技术的特点和差分跳频系统的组网技术，对差分跳频系统的误码率及在高斯白噪声条件下的多用户能力进行了理论分析，同时做出了相应的计算机仿真。仿真结果表明，系统用户数越少相应信噪比条件下的误码率越小，说明干扰越小。

1 差分跳频

相关差分跳频（DFH）通信是近年出现的跳频通信方式。美国Sanders公司研制的相关跳频增强扩谱CHESS电台就采用这种差分跳频技术，实现了在短波波段5 000跳/秒的跳频速率和最高19.2 kbit·s-1的数传速率。

差分眺频的基本原理：当前时刻的工作频率fn由上一跳的工作频率fn-1和当前时刻的信息符号Dn决定，即

fn=G（fn-1,Dn）

其中，G（fn-1,Dn）是一个特定函数，文中称为G函数，它决定了差分跳频的数据/频率映射关系。由此可见，相邻跳变频率之间通过数据序列建立了一定的相关性，亦即相邻频率的相关性携带了待发送的数据信息，因此这种跳频方式也被称为相关差分跳频。

2 差分跳频技术的特点

差分跳频技术集跳频图案、信息调制与解调等功能于一体，构成与传统跳频技术完全不同的技术体制，它具有以下特点：

（1）差分跳频体制是一种相关跳频体制，差分跳频通过G函数变换，使相邻或多跳频率之间具有相关性，其相关性携带了待发送的数据信息，收端也是根据其相关性还原数据信息，所以也将这种跳频体制称为相关跳频。在常规跳频体制中，时间上相邻的频率与其传输的数据信息无关。

（2）差分跳频体制是一种异步跳频体制，差分跳频的收端无法预知每个时刻的发端频率，在工作带宽内进行宽带数字化接收，接收端不需要频率合成器，从这个意义上说，差分跳频是一种异步跳频。

（3）G函数具备数据的调制解调功能，差分跳频无需传统定频或跳频体制中的基带和中频调制，发端经G函数变换，实现数据与频率之间的"数/频"编码，收端先对接收到的直接携带信息的射频频率进行有效检测，再经过G函数的逆变换即可恢复出数据信息，实际这也是一种调制解调过程。相同的情况，这是差分跳频图案产生的机理决定的，普通跳频一般不具备这个特点。

（4）跳频图案没有实时时间参与运算在传统跳频图案产生过程中，除跳频时序控制以外，原始跳频密钥Pk和时间参数TOD参与跳频图案运算。而在差分跳频图案的产生过程中，数据流参与跳频图案的运算，相当于跳频密钥，与实时时间TOD无关。数据流对跳频通信的接收端是未知的。

由于差分跳频与传统跳频的原理有很大差别，造成其组网性能也有很大不同。例如，传统跳频电台组网时，相同频率造成频率碰撞，形成多址干扰，而频率不同时，不构成多址干扰；对于差分跳频电台，不同频率可能会造成接收方数据的误判，从而形成多址十扰；频率相同时，如果削弱有效频率的幅度，则形成多址干扰，如果加强频率的幅度，则不形成多址干扰，与两个频率之间的相位有关。

传统的同步组网是指，各跳频网在技术体制、跳频图案算法及跳频密钥相同以及同一张频率表的条件下，各跳频网每一跳的起跳时刻相同，并且任一时刻的各网瞬时频率正交。由于传统的同步组网是同频造成多址干扰，而差分跳频则是异频可能会形成多址干扰。因此差分跳频同步组网的概念应扩展为在同一张频率表的条件下，各跳频网每一跳的起跳时刻相同时，任一时刻各网瞬时频率不相互形成干扰。差分跳频图案是由随机数据信息控制G函数产生的，而每部电台和各跳频网的数据源是不同的，是相互独立的，相互之间不可能有某种约束关系，导致了即使各台及各网之间在时间上有约束关系，也难以实现各台各网之间频率的人工干预，这样一来，当接收方收到的频率为当前G函数映射出的除当前发送频率之外的m-1个频率中的某一个频点时，就会形成多址干扰。也就是说，要做到差分跳频各网当前跳变频率不落在其余网G函数映射的频率子集之内相当困难。需要通过研究G函数的算法，寻找适当的映射途径，使得各网跳变时刻相同，但任一时刻各网瞬时频率不相互形成多址干扰。

图1为DFH多用户系统模型。每个发射机提供一种交织编码样式，这种编码的码型同数据比特流一起构成传输波形。在每个接收机处，解码器也使用与对应用户相同的码型。如果某接收机对多个发送信号感兴趣，它为合成信号中每个发送信号创建一种检测交织编码样式。其他的发送信号则被认为是干扰，而DFH解码算法能很好地抑制这些干扰。然而某些时候，在已经投入使用的DFH多用户系统中，用户数量会影响解码的性能，而且对干扰的消减程度也是适当的。

图1 DFH多用户系统示例

根据频率数、信噪比、产生一个DFH多用户系统的理论上的误码率γ，以及干扰的数量N-1,并使用多用户信干比SINR为γMU。

在DFH解码的每一阶段，干扰信号会造成模糊概率ρ=（2b-1）/M.换句话说，来自功率为S某一干扰信号的有效的干扰为ps=（2b-1）S/M.因此，如果存在N个功率相等的用户，每个用户都以与无干扰状态下的信噪比γ=S0/N相一致的信号电平来进行传送，这样就可以确定有效的信干比

γMU=γ/（1+γ（2b-1）（N-1）/M） （1）

这样就可以得到高斯白噪声信道条件下的总用户数为N的DFH多用户系统的理论误码率为

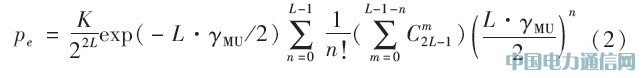
在用户数N=10,b=1的情况下，仿真信噪比随跳频频率个数的变化如图2所示。

图2 M值不同的条件下DFH系统误码率随信噪比的变化

在图2中，画出了用户数为N=10,M=16、M=32、M=64、M=128的条件下，误码率随信噪比的变化曲线。由图可以看出，可用频点数M越高，误码率随信噪比的变化越快，且M越大，相应信噪比条件下的误码率越小，系统性能越好。

设定仿真参数，跳频频率个数M=64,b=1,用户数以2的指数增加，仿真如图3所示。

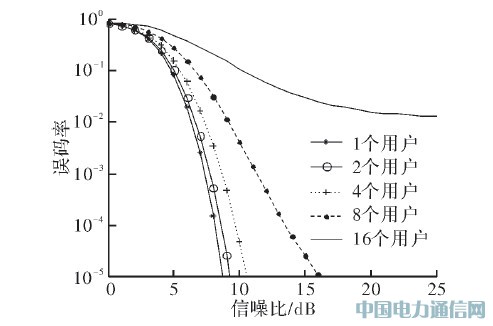
图3 DFH系统在用户数不同的情况下的误码率比较

在图3,中使用Matlab分别画出了用户数N=1、N=2、N=4、N=8、N=16时，DFH系统误码率随信噪比的变化图。由图可以看出，用户越多，DFH系统的误码率越大，信噪比曲线越平缓，即误码率随信噪比变化的速度较慢；用户越少误码率越小，信噪比曲线就越陡峭，即误码率随信噪比变化的速度较快；此外，系统用户数越少，在相应信噪比条件下误码率越小，说明干扰小。

4 结束语

讨论了差分跳频系统的多用户能力，并进行了仿真计算，得出了有益的结论，这将对差分跳频新体制进入实用化有一定的指导意义，为差分跳频组网问题提供了有益的参考，但差分跳频系统的多用户能力还有待于进一步研究，可将其与其他跳频技术的组网能力进行比较研究。