摘要: 自平衡机器人、多旋翼无人飞行器的控制需要高精度的姿态运动信息作为反馈输入,要求测量模块具有响应快、体积小和功耗低的特点。采用低成本的MEMS器件与STM32单片机构建了航向姿态参考系统硬件平台。针对传感器的特点,设计了基于扩展卡尔曼滤波算法的双矢量校正方法,并给出了陀螺仪的温度补偿、磁传感器的校正方法。
引言
航向姿态参考系统(Attitude and Heading Reference System,AHRS)能够提供航向、横滚和侧翻等姿态信息,机械陀螺仪及光纤陀螺仪等高精度惯性导航器件价格昂贵,难以得到推广。目前MEMS传感器在消费类电子产品中得到广泛应用,但是MEMS角速率陀螺仪存在严重的零点漂移和随机误差,在捷联惯性导航解算中会产生积分误差,难以达到应用的精度。加速度计和磁场计能分别测量出重力加速度和地磁场这两个不相关的三维矢量,可以作为平台姿态的观测矢量来校准陀螺仪。扩展卡尔曼滤波可以结合这几种传感器的特点,以陀螺仪测量得到的角速率作预测更新,以重力加速度和磁场观测更新,得到更高精度的姿态角信息。
1 硬件结构
MEMS器件的AHRS硬件基本组成为三轴角速率陀螺仪、三轴加速度计、三轴磁阻传感器和STM32系列微处理器STM32F103U8T6。航向姿态参考系统的硬件结构如图1所示。
IMU采用整合了16位的三轴陀螺仪和三轴加速度计的MPU6000,与多组件方案相比,有效避免了组合陀螺仪与加速器时之轴间安装误差的问题,节省了安装空间。同时,内部自带了16位A/D转换器,简化了电路设计。MPU6000的角速率量程为±250 °/s、±500 °/s、±1000 °/s与±2000 °/s。加速度测量范围为±2g、±4g、±8g与±16G。内部自带16位的数字温度传感器,方便对传感器进行温度补偿。数据可通过最高可达400 kHz的I2C总线或最高可达20 MHz的SPI接口传输,采样更新速率达到8 kHz,可保证系统测量的实时性。
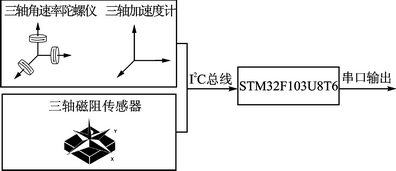
图1 航向姿态参考系统的硬件结构
霍尼韦尔HMC5883为三轴12位I2C总线数字量输出磁阻传感器,测量范围为±1~±8 Gs,数据更新速率为80 Hz。内置OFFSET/SET/RESET电路,不会出现磁饱和与累加误差现象,支持自动校准程序,简化使用步骤,可以满足地磁场的测量要求。选用基于CortexM3内核的STM32系列ARM处理器STM32F103U8T6,主频达72 MHz,1.25 DMIPS/MHz;具有硬件单周期乘法器,保证姿态更新的实时性;具有丰富外设接口,可采用I2C总线接口从传感器中读取数据,通过串口与上位机进行通信。
2 四维扩展卡尔曼滤波算法
扩展卡尔曼滤波算法(Extended Kalman Filter, EKF)是一套由计算机实现的实时递推算法,所处理的对象是随机信号,利用系统噪声和观测噪声的统计特性,以系统的观测量作为滤波器的输入,以所要求的估计值(系统的状态变量)作为滤波器的输出,滤波器的输入和输出由时间更新和观测更新算法联系在一起,根据系统的状态方程和观测方程估算出所需要处理的信号。AHRS扩展卡尔曼滤波算法的状态变量采用四维四元数,与采用欧拉角相比,避免了采用欧拉角计算时涉及的大量三角函数运算,保证了更新速率和实时性,同时不存在采用欧拉角运算出现的奇异性。欧拉角与四元数的转换关系如式(1)~(3)所示。
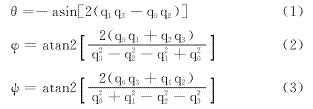
四元数微分方程如式(4)所示,四元数姿态矩阵微分
方程只要解4个微分方程,比方向余弦姿态矩阵微分方程减少了大量的运算,便于微处理器的编程实现。
2.1 时间更新
系统的状态方程如式(5)所示。
其中状态变量为四元数X=[q0,q1,q2,q3]T,Wk-1为四维过程噪声。矩阵A可以根据陀螺仪测得的三轴角速率[ωX,ωY,ωZ]T得到,如式(6)所示。其中Δt为两次时间预测更新所流逝的时间。
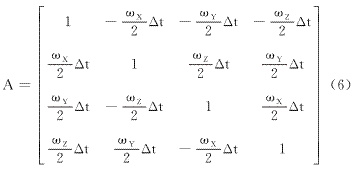
状态变量的时间更新如式(7)所示。
协方差矩阵P预测如式(8)所示,式中Q为四维过程激励噪声协方差。
2.2 观测更新
AHRS的观测更新是通过本体坐标系上的重力加速度和地磁场的参考矢量旋转至导航坐标系上,再与加速度和磁场传感器比较,得到观测变量的残余。由本体系转换至导航系的转移矩阵由四元数可以表示为式(9)。
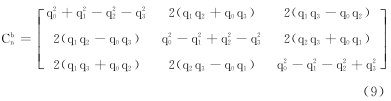
三维参考向量v转移至导航系中可由观测方程式(10)表示。
当重力加速度观测更新时参考向量v等于重力加速度参考矢量(可设置为当平台静止水平放置时,加速度计测量得到的三维矢量为:
当磁场观测更新时v等于磁场参考矢量(可设置为当平台静止水平放置且航向指向正北时,磁阻计测量得到的三维矢量为:
H是h对X求偏导的雅可比矩阵,如式(11)所示。
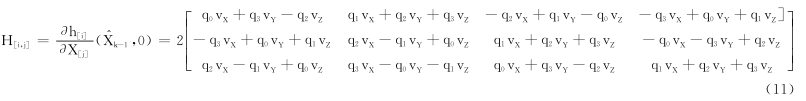
卡尔曼增益矩阵Kk如式(12)所示,式中R阵为三维观测噪声协方差矩阵。
观测更新:
当重力加速度观测更新时zk为加速度,传感器测量得到的三维矢量zk=[aXaYaZ]T,当磁场观测更新时zk为磁阻传感器,测量得到的三维矢量zk=[mXmYmZ]T。协方差更新:
3 程序结构
AHRS的软件设计主要分为:
① 传感器初始化,包括设置传感器的更新速率、量程。
② 初始化卡尔曼滤波的相关矩阵,根据传感器的特点设置过程激励噪声协方差矩阵Q,设为对角元素为0.1的四维对角方阵。
③ 若成功读取陀螺仪数据,进行卡尔曼滤波的时间更新。
④ 采集加速度传感器和磁阻传感器的数据,若读取成功则进行观测更新。加速度观测更新与磁场观测更新算法差别在于观测方差的R,可根据两种传感器的置信度设置相应的值,航向姿态参考系的程序流程如图2所示。
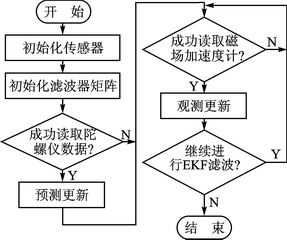
图2 航向姿态参考系的程序流程
4 传感器校准
4.1 陀螺仪温度补偿
低成本MEMS陀螺仪存在着较大的零点偏移,一般可以达到1~3 °/s。可以通过增加扩展卡尔曼滤波的状态变量的维数,即增加三维陀螺零偏做数据融合得以解决。优点是可以动态地估计陀螺的零偏,有较强的适应能力,缺点是卡尔曼滤波算法的计算量以维数的三次方增加,因此实时性会有所降低,在要求姿态更新速率高而单片机计算性能有限的情况下,可以采用温度补偿的方法解决。陀螺仪的零点偏移与传感器温度和温度梯度密切相关。MPU6000陀螺仪温度变化缓慢的情况下,可以认为其温度零点漂移对应此时传感器的温度。
可设温漂曲线为三次多项式BX=At3+Bt2+Ct1+D,通过最小二乘法拟合之后可得到各项系数。经过温度补偿后的陀螺仪曲线如图3所示。
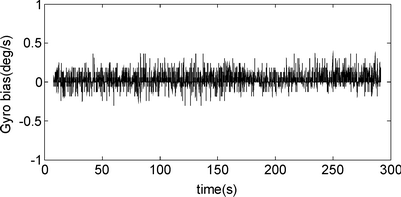
图3 静止时减去温漂后的角速率曲线
4.2 硬磁及非正交度校正
地磁场正常情况下测量到的三维数据在空间上的包络应该是一个标准的圆球。但是磁场计测量出来的数据由于受到外界磁场的影响,加上磁阻传感器各轴的标度因子和非正交度,导致传感器采集到的数据在三维空间内分布的包络面为球心偏移原点的椭球面,磁场裸数据三维分布如图4所示。
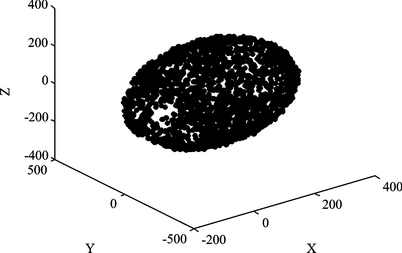
图4 磁场裸数据三维分布
椭球面约束方程如式(15)所示。
其中m为传感器测得的三维磁场强度,c为球心偏移的三维向量,U为标度因子及非正交度校矩阵。磁场强度没有实际意义,关心的是传感器测量的地磁三维矢量方向,所以设磁场向量模为1。通过最小二乘法可以计算出U和c。磁场数据校正前后对比如图5所示,左右两图为校正前后数据在XY平面上的投影。
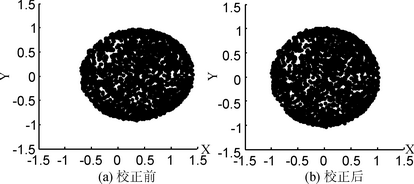
图5 磁场数据校正前后对比
5 实验结果
AHRS放置在与1024线光栅编码器固连的转动平台上,测试俯仰姿态角的测量精度及跟踪性能,AHRS与编码器测量曲线对比如图6所示。
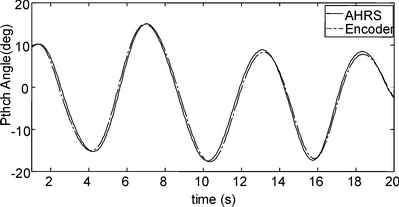
图6 AHRS与编码器测量曲线对比
图中实线为AHRS的测量值,点划线为编码器的测量值。当测试平台以幅度约±10°的幅度摆动时。AHRS与编码器测量数据相比在时间上滞后最大不超过5 ms,峰峰值相差不超过03°。
结语
基于四元数扩展卡尔曼滤波算法的AHRS具有更新速率高、实时性好、价格低廉的特点,能够广泛应用于手机、平板电脑等消费类电子产品, 也能满足一些机器人对姿态控制的测量需求。
参考文献
[1] 付梦印,邓志红,闫莉萍.Kalman滤波理论及其在导航系统中的应用[M].2版.北京:科学出版社,2010:1718.
[2] 毛奔,林玉荣.惯性器件测试与建模[M].哈尔滨:哈尔滨工程大学出版社,2007:9394.
[3] 邓正隆.惯性技术[M].哈尔滨:哈尔滨工业大学出版社, 2006:620.
[4] 李建利.新型硅MEMS陀螺仪和角加速度计结构设计及MIMU误差标定补偿[D].北京:北京航空航天大学,2008.
[5] C C Foster, G H Elkaim, UC Santa Cruz. Extension of a twoStep calibration methodology to include nonorthogonal sensor axes[J]. IEEE Transactionson Aerospace and ElectronicSystems, 2008,44(3):10701078.
[6] 张树侠.捷联式惯性导航系统[M].北京:国防工业出版社,1992:1517.
[7] 吴永亮,王田苗,梁建宏.微小型无人机三轴磁强计现场误差校正方法[J].航空学报, 2011, 32(2):330336.
梁建宏(讲师),主要研究领域为小型无人机。 