(中国民航大学计算机科学与技术学院,天津 300300)
0 引言
得益于传感器及监控技术的进步,现代工业设备的生产运行状态和运行环境能够被实时记录和感知,积累并产生了海量多维时间序列(MTS,multivariate time series)数据[1]。例如,云服务器的CPU利用率、内存占用率、网络流量等监测数据,航空器的速度、高度、俯仰角度等传感器数据,反映航天器运行状态的遥测信号,工厂生产机器的温度、转速等监测数据。这些MTS 数据的异常取值片段往往意味着设备故障、操作人员失误等特殊情况的发生,也可能表示生产环境中存在隐性安全隐患。这些异常如不能被有效识别,很可能造成经济损失。工业领域MTS 数据有如下特点:体量大、连续采样、价值密度低、动态性强;MTS 各维度之间具有复杂的时空耦合关系;工业设备通过其软件控制逻辑往往与其运行环境、操作人员及相关设备系统有复杂交互,反映其运行状态的MTS 取值具有随机性[2]。另外,由于工业领域MTS 异常样本相对较少、标注异常代价较高,研究者大多关注基于无监督的MTS异常检测方法。传统的主成分分析、高斯混合模型、一类支持向量机等机器学习方法无法很好地建模工业领域MTS 数据的复杂性质。由于深度学习强大的数据表征能力,近年来,基于深度学习的无监督MTS 异常检测研究得到了广泛关注。MTS 异常检测包括序列级和瞬时级异常发现。序列级异常[3-5]是指MTS 样本整个序列或其子序列区别于多数样本。瞬时级异常是指在某个时间点或短时间窗内的异常。本文模型属于瞬时级异常检测模型。
围绕如何建模工业领域MTS 时序依赖性和随机性,研究者提出了一些深度学习模型[2,6-10]。这些模型的训练目标均为学习正常MTS 样本集的时序分布。其中,大部分方法均结合循环神经网络(RNN,recurrent neural network)和变分自编码器(VAE,variational autoencoder)建模MTS 数据的时序依赖性和随机性。但已有模型存在如下问题。
1) 采用RNN 的隐向量实现VAE 隐空间中随机变量间的时序依赖性,然而RNN 难以捕获序列数据的长时依赖性,这降低了学习序列数据分布的能力。
2) 计算随机变量的近似后验分布和先验分布的网络结构相同,这使2 种分布KL 散度(Kullback-Leibler divergence)距离较小,增加了模型的训练难度。基于线性高斯状态空间模型(LGSSM,linear Gaussian state space model)计算随机变量的先验分布无法实现随机变量间的非线性转换。
3) 基于RNN 的生成网络仅依赖于随机变量的采样值,没有利用RNN 推断网络的确定性隐向量。
针对以上问题,本文提出一种面向工业领域MTS 异常检测的随机Transformer(ST-MTS-AD,stochastic Transformer for MTS anomaly detection)模型。该模型由Transformer 编码器输出的表示各时刻MTS 长时依赖特征和上一时刻随机变量的采样值生成当前时刻随机变量的近似后验分布,使ST-MTS-AD 可借用Transformer 编码器输出的长时依赖特征在隐空间中传播随机变量间的长时依赖性,采用门控转换函数(GTF,gated transition function)生成随机变量的先验分布并实现随机变量间的非线性转换,通过将Transformer 编码器输出的长时依赖特征和随机变量采样值输入多层感知器(MLP,multilayer perceptron)重构MTS 各时刻取值分布。在4 个工业领域公开MTS 数据集上的实验表明ST-MTS-AD 具有较好的异常检测效果。
1 相关研究现状
多维时间序列异常检测是时间序列分析领域中的重要任务之一,旨在寻找不符合规则的或出现偏差的序列片段[11]。目前,基于深度学习的MTS瞬时级异常检测方法如下。
1) 基于预测和重构的确定性方法。Hundman等[12]设计了基于长短时记忆(LSTM,long short-term memory)网络的航天器遥测信号异常检测方法,通过预测误差确定异常,其还提出了一种非参数动态异常检测阈值确定方法,能在误报率和漏报率之间达到平衡。Zhang 等[13]提出了面向多传感器MTS 异常检测的深度卷积自编码记忆网络,将MTS 的时空嵌入表示和重构误差输入线性自回归模型和基于注意力机制的双向LSTM 网络,由重构损失和预测损失确定MTS 异常。Malhotra 等[14]提出了一种基于LSTM 的自编码器模型,旨在重建正常时间序列,使用重构误差进行异常检测。Zhang等[15]提出了一种多尺度卷积循环自编码器(MSCRED),首先构建能表征MTS 不同变量间相关性的多尺度签名矩阵;然后采用卷积编码器对签名矩阵进行编码,使用基于注意力的卷积LSTM 捕获MTS 时序依赖性;最后基于卷积解码器重建签名矩阵,并利用签名矩阵的重构误差诊断异常。Audibert 等[16]设计了包含一个编码器和2 个解码器的自编码器网络结构,采用对抗学习策略训练网络,避免自编码器无法通过重构误差区分正常样本与异常样本的现象,该方法没有使用循环神经网络从而获得了较快的训练效率,但无法建模MTS 的时序依赖关系。上述方法以预测或重构为训练目标刻画正常MTS 样本的特征,由重构误差和预测误差检测MTS 异常,无法建模MTS 的随机性。
2) 基于重构的随机性方法。Zong 等[6]提出一种用于无监督异常检测的深度自编码高斯混合模型(DAGMM,deep autoencoding Gaussian mixture model),通过自编码器获得训练样本的低维表示,将低维表示和样本重构误差拼接形成的向量输入用来训练GMM 参数的估计网络,由GMM 模型计算的样本能量值确定样本是否异常。Deng 等[7]采用图卷积网络捕获MTS 变量间交互特征,由自注意力机制提取MTS 长时依赖特征,基于VAE 的重构能力进行MTS 异常检测。Park 等[8]提出了基于LSTM 和VAE 的多模态MTS 异常检测方法,以LSTM 网络结构作为VAE 中的生成网络和推断网络表示MTS 的随机性和时序依赖性。文献[7-8]通过自注意力机制或RNN 捕获MTS 的时序依赖性,并且每个时间点通过重参数化采样得到的随机变量具有随机性,但随机变量之间没有时序依赖性。
为此,研究者提出了基于VAE 的序列数据生成模型[17-19],这些方法均采用变分推断技术学习时序数据分布,并且可以表示随机变量间的时序依赖性。Chung 等[18]提出一种变分循环神经网络(VRNN,variational recurrent neural network)模型。VRNN的推断网络由时序数据当前时刻输入值和上一时刻RNN 隐向量生成当前时刻随机变量的近似后验分布。VRNN 通过RNN 隐向量的迭代更新实现随机变量间的时序依赖性。VRNN 的生成网络由当前时刻随机变量采样值和上一时刻RNN 隐向量生成时序数据取值分布。Dai 等[9]提出了面向内容分发网络系统多元关键性能指标时序数据的异常检测方法SDFVAE(static and dynamic factorized VAE),将VRNN 中的随机变量分解为动态和静态随机变量,其中,静态随机变量刻画内容分发网络系统性能指标取值的时序不变性。SDFVAE 由双向LSTM网络学习静态随机变量的近似后验分布,动态随机变量的近似后验分布生成方式与VRNN 相同。Li等[10]提出了基于VRNN 的MTS 异常检测方法,在损失函数中引入使相邻时刻点时序取值生成分布相近的正则化项,使模型具有更好的抗噪能力。Fraccaro 等[19]提出了一种融合状态空间模型(SSM,state space model)和RNN 的随机循环神经网络(SRNN,stochastic recurrent neural network)。SRNN模型通过依赖于RNN 隐向量和SSM 随机变量采样值的神经网络实现SSM 随机状态之间的非线性转换,使SSM 可以利用RNN 表示时序依赖关系的隐向量在隐空间中传播随机性。SRNN 与VRNN 的区别在于RNN 隐向量的更新不依赖于各时刻的随机变量,能直接建模每个时刻随机变量间的时序依赖性,实现了RNN 确定性隐变量和SSM 随机变量的分离。文献[19]表明SRNN 能够比VRNN 更好地学习时序数据的分布。Su 等[2]提出基于SRNN 的MTS异常检测模型,该模型的推断网络结构与SRNN 相同,在此基础上采用平面归一化流技术学习各时刻非高斯分布的近似后验分布。在生成网络中,该模型由依赖于随机变量采样值的RNN 生成时序数据取值分布,采用LGSSM 计算随机变量的先验分布并实现随机变量间的时序依赖性。
2 ST-MTS-AD 模型设计
2.1 相关符号定义及ST-MTS-AD 网络结构
MTS 数据集记为k=[k1,k2,…,kN] ∈RM×N,N为k的持续时间长度,每个观测值kτ∈RM是在时间点τ(τ≤N)的M维向量。使用窗口大小为w、滑动步幅为l的滑动窗口对k进行预处理,每个滑动窗口为
本文设计的ST-MTS-AD 模型基于VAE 的变分推断技术学习MTS 时序分布,其主要优势在于使用Transformer 编码器中的多头自注意力机制生成MTS各个时刻点的随机分布,实现了VAE 隐空间中随机变量间的长时依赖关联。而且ST-MTS-AD 的生成网络为MLP,降低了模型的复杂性。ST-MTS-AD 模型结构如图1 所示。在推断网络中,Transformer 编码器将观测序列x1:T∈RP×T映射为特征e1:T=[e1,…,et,…,eT] ∈Rd×T,d为Transformer 编码器输出维度,e1:T捕获x1:T中观测变量xt间的长时依赖性,et(1 ≤t≤T)表示e1:T在t时刻的取值向量。将t-1 时刻随机变量zt-1的采样值和et串接后输入MLP 生成t时刻随机变量zt的近似后验分布,实现随机变量zt-1和zt的非线性转换和时序依赖关联。记T个随机变量z1,…,zT为z1:T。在生成网络中,t时刻随机变量zt采样值和取值向量et输入MLP 生成的取值分布。T个时刻观测变量xt的重构值,…,表示为。t-1 时刻随机变量zt-1的采样值输入GTF生成t时刻随机变量zt的先验分布,z0为随机初始化的向量。ST-MTS-AD 通过最大化证据下界优化推断网络和生成网络参数,由各时刻x′t的重构概率似然确定x1:T异常片段。
2.2 ST-MTS-AD 推断网络设计
Transformer 网络中的自注意力机制容易捕获序列数据中长时依赖特征,文献[20]基于Transformer 编码器设计了MTS 的高质量表示学习模型。ST-MTS-AD 模型将Transformer 编码器作为VAE 的推断网络,捕获观测序列x1:T中各观测变量xt间的长时依赖性。为了实现随机变量zt-1和zt的非线性转换和时序依赖关联,将t-1 时刻随机变量zt-1的采样值和Transformer 编码器在t时刻的输出et串接后生成t时刻随机变量zt。推断网络的目标是学习随机变量z1:T的真实后验分布,ST-MTS-AD通过推断网络得到z1:T的近似后验分布,如式(1)所示。
ST-MTS-AD 模型推断网络结构如图2 所示,即式(1)中t时刻近似后验分布网络结构。
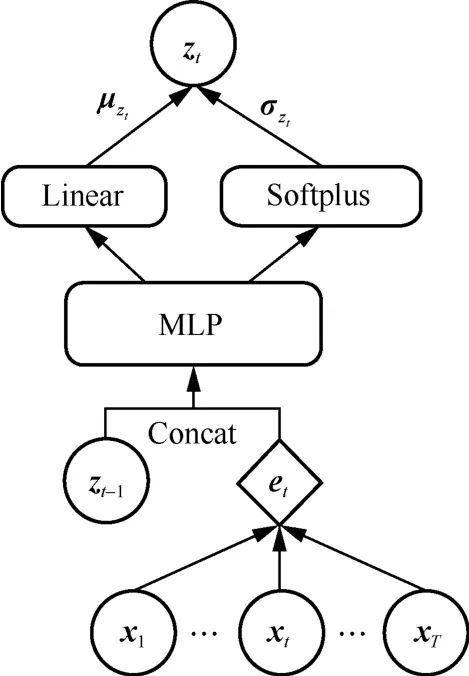
图2 ST-MTS-AD 模型推断网络结构
e1:T计算过程如下。按式(2)对x1:T进行位置编码,编码结果记为。
其中,Wx∈Rd×P为网络参数;b∈R1×T为偏置项;wp∈Rd×T为位置编码矩阵,由正弦函数在偶数位置计算得到的位置信息和余弦函数在奇数位置计算获得的位置信息结合形成,具体形式如下
由式(4)~式(10)所示的多头注意力机制计算x1:T中观测变量间长时依赖特征e1:T。
2.3 ST-MTS-AD 生成网络设计
ST-MTS-AD 生成网络由MLP 构成,目的是重构观测序列。其与文献[2,9]不同之处在于,由随机变量zt采样值和推断网络中Transformer 编码器在t时刻的输出et生成t时刻的观测变量,而不仅依赖随机变量zt。这是由于et包含了来自输入观测序列x1:T的全局时序特征,能够更好地重构观测序列。同时,MLP 网络结构简单,降低了ST-MTS-AD 网络的复杂性。ST-MTS-AD 生成网络的联合概率分布为
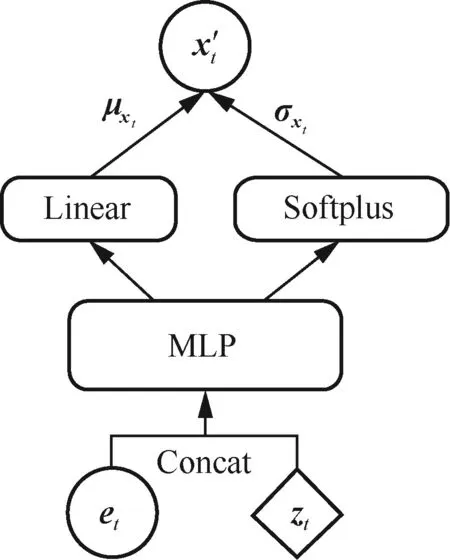
图3 ST-MTS-AD 模型生成网络结构
其中,ξ~N(0,I),⊙表示向量元素乘积,和分别表示由图2 推断网络生成的zt近似后验分布均值和标准方差。
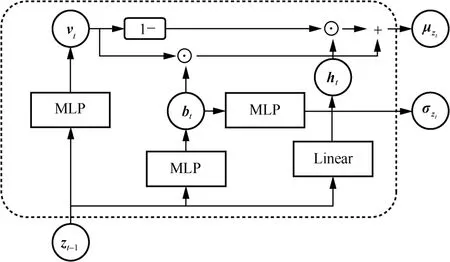
图4 GTF 网络结构
式(16)表示具有ReLU 和Sigmoid 激活函数的MLP,式(17)表示具有ReLU 激活函数的MLP,式(18)表示Linear 层,式(20)表示具有ReLU 和Softplus 激活函数的MLP。
2.4 优化目标
ST-MTS-AD 模型的优化目标为最大化式(21)所示的证据下界(ELBO,evidence lower bound)。
算法1ST-MTS-AD 模型的训练算法


3 实验
3.1 实验数据集及环境
实验采用以下4 个公开的数据集:SMD(server machine dataset)来自一家大型互联网公司为期5 周的服务器检测数据集[2];MSL(mars science laboratory)和SMAP(soil moisture active passive satellite)来自NASA 航天器监测系统报告中的遥感数据[12];SWaT(secure water treatment)来自一个水处理厂信息物理系统为期11 天的监控数据集[3]。各数据集具体的描述如表1 所示。
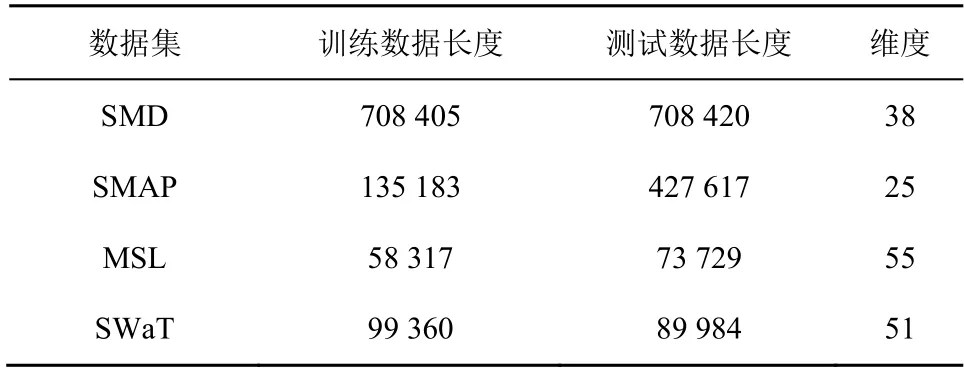
表1 各数据集具体的描述
实验硬件环境如下:Ubuntu16.04 操作系统,Inter Xeon Gold 5220R CPU,NVIDIA Tesla T4 显卡。软件环境如下:Python3.6,Pytorch 1.10.1。
3.2 实验模型参数设置和评价指标
ST-MTS-AD 模型在SMD、SMAP、MSL、SWaT数据集上的滑动窗口大小w、滑动步幅l、观测序列长度T和自注意力头数H分别设为10、10、200和8。根据数据集的维度大小,模型在SMD 和SWaT数据集上的Transformer 编码器输出维度d分别设为128 和256,在SMAP 和MSL 数据集中设为64。实验使用Adam 优化器,设置学习率r=0.000 1,批处理大小batch=64,训练周期数epoch=200。
ST-MTS-AD 目标是检测观测序列x1:T中观测变量xt是否异常。在测试集中,若观测变量xt表示的滑动窗口中某一时间点取值kτ∈RM为异常点,则xt标记为异常。对于测试集中的每个观测变量xt,如果重构出的观测变量被判断为异常,且xt真实标签也为异常,则记为真阳(TP)。如果重构出的观测变量被判断为异常,但xt真实标签为正常,则记为假阳(FP)。如果重构出的观测变量被判断为正常,但xt真实标签为异常,则记为假阴(FN)。如果重构出的观测变量被判断为正常,且xt真实标签为正常,则记为真阴(TN)。本文使用3 个指标来衡量异常检测模型的性能,分别为精确率Precision、召回率Recall、F1 分数,其中,F1 分数为精确率和召回率的调和平均数,F1分数越大表示异常检测模型的性能越好。
3.3 实验结果与分析
选取6 种与ST-MTS-AD 相关的异常检测模型进行实验对比,分别为DAGMM[6]、LSTM-VAE[8]、MSCRED[15]、USAD(unsupervised anomaly detection)[16]、OmniAnomaly[2]、SDFVAE[9]。各模型的实验均采用本文的数据预处理方式,不同模型的性能对比如表2 所示。
从表2 可知,ST-MTS-AD 模型在SMD、SMAP、MSL 和SWaT 数据集上的F1 分数分别为0.933 2、0.966 4、0.981 9 和0.834 2,相较于5 种对比模型整体上有较高的提升。在SMD、SMAP、MSL 和SWaT数据集上,ST-MTS-AD 模型的F1 分数比MSCRED分别提高了15.6%、10.0%、4.7%和3.3%,ST-MTS-AD模型的F1 分数比USAD 模型分别提高了9.6%、6.9%、15.6%和3.0%,与MSCRED 相比,ST-MTS-AD 在SMD 数据集上的F1 分数提高最多,这是因为SMD数据集中存在持续时间短、异常偏差较小的取值片段[9],MSCRED 模型中的构造签名矩阵无法捕获这些细微的异常特征。USAD 虽然采用对抗学习策略避免自编码器无法通过重构误差区分正常样本与异常样本的问题,但其自编码器网络没有捕获MTS 的时序依赖特征。实验结果也验证了基于重构的随机性模型ST-MTS-AD 的异常检测效果好于基于重构的确定性模型MSCRED 和USAD。
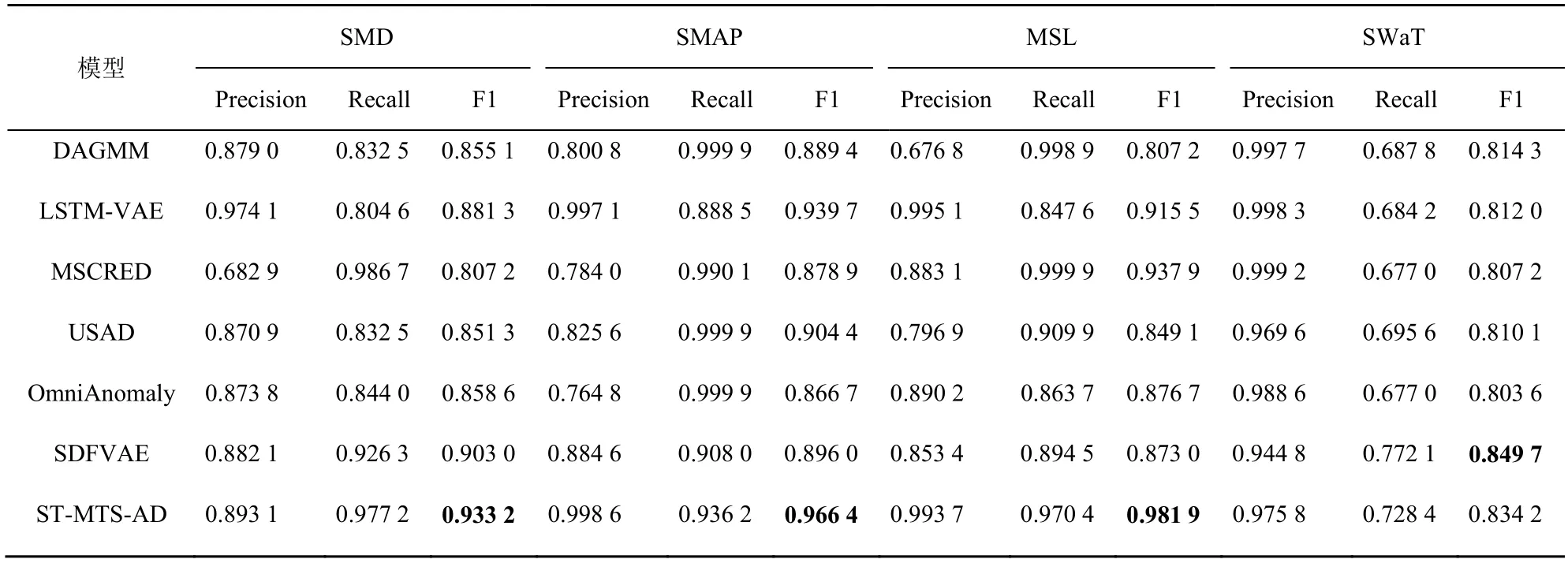
表2 ST-MTS-AD 模型与6 种模型的性能对比
DAGMM 的F1 分数在SMD、SMAP、MSL和SWaT 数据集上比ST-MTS-AD 模型分别低8.4%、7.9%、17.7%和2.3%,DAGMM 虽属于基于重构的随机性模型,但其自编码器网络结构设计面向表格数据,无法提取 MTS 时序特征。ST-MTS-AD 模型在SMD、SMAP 和MSL 数据集上的F1 分数比SDFVAE 分别提高了3.3%、7.8%和12.4%,但在SWaT 数据集上的F1 分数比SDFVAE 低 1.8%,这是由于SDFVAE 比ST-MTS-AD 模型有较强的抗噪能力。LSTM-VAE和OmniAnomaly为与ST-MTS-AD最相关的模型,均为基于VAE 的序列生成模型。在SMD、SMAP、MSL 和SWaT 数据集上,ST-MTS-AD 模型的F1分数比LSTM-VAE 模型提高了5.9%、2.8%、7.3%和2.7%,比OmniAnomaly 模型提高了8.6%、11.5%、11.9%和3.8%。这是由于LSTM-VAE 模型无法建模隐空间中随机变量之间的时序依赖性。OmniAnomaly 模型基于RNN 各时刻的隐向量实现随机变量间时序依赖性,这种机制无法实现随机变量间的长时依赖关联,其采用的基于LGSSM 的随机变量先验分布生成方式无法实现随机变量间的非线性转换,且该模型在生成网络中仅依赖各时刻随机变量的采样值,没有利用推断网络RNN 的隐向量信息。
3.4 消融实验
为了验证ST-MTS-AD 模型相关模块设计的有效性,将ST-MTS-AD 模型与其3 个变体进行对比,3 个变体分别为ST-MTS-AD-1、ST-MTS-AD-2 和ST-MTS-AD-3。ST-MTS-AD-1 模型表示在图1 的ST-MTS-AD 模型基础上将推断网络中Transformer编码器替换为门控循环单元(GRU,gate recurrent unit)神经网络。ST-MTS-AD-2 模型表示将ST-MTS-AD 模型中用于生成随机变量先验分布的GTF 替换为LGSSM。ST-MTS-AD-3 模型表示图1生成网络去除了et作为输入的设计,生成网络的输入仅来自随机变量zt的采样值。各模型在4 个数据集上的实验结果如图5 所示。
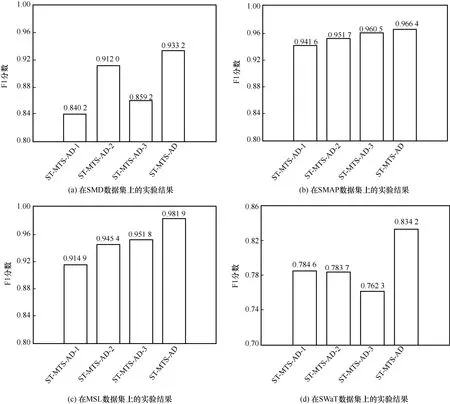
图5 不同数据集上的消融实验
从图5 可知,ST-MTS-AD 模型在SMD、SMAP、MSL 和SWaT 数据集上的F1 分数比ST-MTS-AD-1模型分别提高了11.1%、2.6%、7.3%和6.3%,因此基于Transformer 编码器生成的时序依赖特征能更好地实现隐空间中随机变量间的时序依赖性。ST-MTS-AD 模型的F1 分数比ST-MTS-AD-2 模型分别提高了2.3%、1.5%、3.9%和6.4%,原因是GTF采用GRU 的思想对随机变量zt-1到zt的转换函数进行参数化,通过非线性转换函数控制zt-1到zt的信息传递,可以捕获随机变量之间更复杂的依赖性,而LGSSM 利用卡尔曼滤波的思想实现随机变量间的线性转换,结果证明了ST-MTS-AD 使用GTF的连接方式比使用LGSSM 的连接方式更加有效。ST-MTS-AD 模型的F1 分数在SMD、SMAP、MSL和SWaT 数据集分别比ST-MTS-AD-3 模型提高了8.6%、0.6%、3.2%和9.4%,由Transformer 编码器生成长时依赖特征et和推断网络生成的随机变量zt的采样值能更好地重构MTS 各时刻x′t的分布。另外,与ST-MTS-AD-1、ST-MTS-AD-2 和ST-MTS-AD-3相比,ST-MTS-AD 在SMAP 数据集上的的F1 分数提高并不明显。这是因为SMAP 数据集中存在很多离散变量,其异常片段比较容易被检测。
4 结束语
本文提出了一种融合Transformer 编码器和VAE 的随机Transformer MTS 异常检测模型。该模型基于Transformer 编码器生成的时序特征实现隐空间中随机变量间的长时依赖性,采用门控转换函数生成时序随机变量的先验分布,由推断网络生成的各时刻随机变量近似后验分布采样值和Transformer 编码器输出的时序特征重构MTS 各时刻取值的分布。在4 个公开数据集上实验结果表明了ST-MTS-AD 设计的有效性。下一步笔者将研究如何基于Transformer 编码器实现隐空间中随机变量间的非马尔可夫动态性。