目标雷达信号可能是宽带信号,系统波段可能进一步扩展。由于馈源尺寸不能无限度地缩小,系统带宽、馈源尺寸、馈源间距将成为相互矛盾的需求,为了解决这个困难,拟在阵面左右两侧采用非等距间距,比如在右侧采用3/2波长间距,而左侧采用4/2波长的间距,利用间距的3与4互质的关系,可进行角度解模糊,获得真实的信号到达角。
1 非等距间距解模糊条件证明
利用测量所得阵元间的相位差φi(θ),可根据孙子定理惟一确定无模糊信号DOA。
孙子定理基本原理:

b1,b2,…,bs为余数,当m1,m2,…,ms为两两互质的整数时,对任意的整数b1,b2,…,bs,总有整数解x,且此解在模m=m1,m2,…,ms意义下惟一。其解可通过如下方法求得。
记Mi=m/mi,先求ui使:
uiMi≡1 mod(mi) 1≤i≤s
则有:
u1M1+u2M2+…+usMs≡1 mod(m)
令ei=uiMi,i=1,2,…,s,则孙子方程式的解为:
x≡b1e1+b2e2+…+bses mod(m)
利用孙子定理解DOA模糊的基本思路是:
选择两两互质的阵元间距di(与定理中的mi对应),根据测量所得的阵元间相位差φi(θ)(与定理中的bi对应),则可利用孙子定理惟一确定无模糊DOA(与定理中的x对应)。
因为两阵元间相位差φ(θ)=2 πdi/λsinθ,在无模糊测相条件下,d=λ/2,因此φ(θ)=πsinθ。式中,测量值φ在-π~π变化,sinθ从-1~1变化,结果如图1所示。φ对sinθ是一条直线,具有一一对应关系,不产生角度模糊。
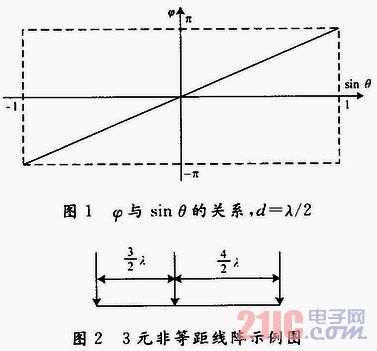
因为sinθ∈[-1,1],则φ∈[-3π,3π],但由于实际测量所得的相位差φ∈[-π,π],任何超过这一范围的角度φ’都将折算进这一范围。即:
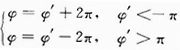
对于每一个φ值,都有3个相应的sinθ,即有3个角度与之对应,从而存在角度模糊。不可能通过一对阵元来确定信号的DOA。与图1相比,图3中直线的斜率要大些,因此分辨率要高些。
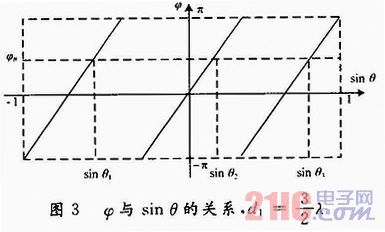
为了解决模糊问题,需要另外一对间距为的天线,其结果如图4所示。图中对任意的信号入射角θ,将有两个特殊的φ1,φ2与之对应,因此,只需测得φ1,φ2,即可求得入射角θ。阵元间距间的两两互质,保证了图中φ1,φ2和θ间的一一对应关系。

2 非等距线阵空间傅里叶变换
2.1 阵列模型
将70个阵元分为两部分,设入射角为15°。第一部分M1=30,阵元间距为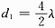 ,第二部分M2=40,阵元间距
,第二部分M2=40,阵元间距 ,如图5所示。由于阵元间距超过波长的1/2,所以存在角度模糊,根据非等距线阵解模糊条件可知,此时d1与d2互质,满足条件,可以进行解模糊。
,如图5所示。由于阵元间距超过波长的1/2,所以存在角度模糊,根据非等距线阵解模糊条件可知,此时d1与d2互质,满足条件,可以进行解模糊。
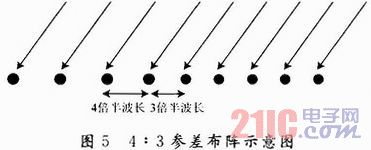

矩阵的M列分别表示线阵天线的M个阵元,N行分别表示接收端信号高速采集卡以一定采样频率在信号一个脉冲周期中采集到的N个采样点。
对接收信号矩阵的每一列作N0点的FFT(N≤N0),得到各阵元接收宽带信号x(n)的离散频谱,可表示为:
2.2 插值对齐
通过观察不难发现,矩阵中每行上相邻元素,前30个阵元的相位相差为2πd1sinγ/λi,后40个阵元的相位相差为2πd2sinγ/λi,这是由于线阵天线阵元在空间等距延伸分布,使得接收信号在传播过程中形成固定路径差,从而导致相位差。这样,对于矩阵中每行元素组成的序列,可以等效地看作信号频率为sinγ成正比的单频信号,以等效采样频率λi/d1,λi/d2欠采样得到的空间频率采样点。
前30个元素相当于对信号频率为sinγ成正比的单频信号进行4倍抽取,后40个元素相当于对信号频率为sinγ成正比的单频信号进行3倍抽取,对前30个元素每个元素间内插3个0进行FFT变换,对后30个元素每个元素间内插2个0进行FFT变换。
两部分波束后的角度模糊分别有四个和三个栅瓣,把模糊角度的栅瓣对齐后,将两部分对比,在相同位置有峰值的角度即为解模糊角。栅瓣波束方向图如图6所示。
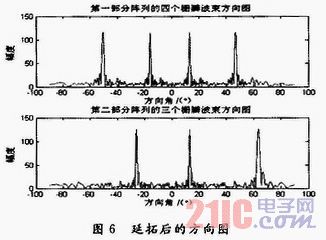
对两部分阵列相加和相减后对齐,进行解模糊,如图7所示。
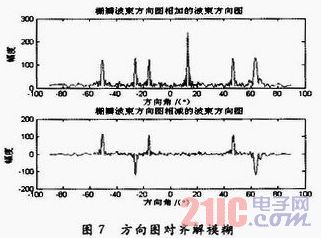
可以从图7中发现,对齐的位置相加后幅度最大,相减后在所有峰值处最接近于零,估计的角度为15°。
设接收信号矩阵各行分别对前后两部分按欠采样率补0后分别作相应点数的FFT后得到矩阵:

3 方法总结
如果按照窄带信号的波达方向估计方法,就是在上式中矩阵每行找出模平方最大的元素,找出其对应的sinγ值,进而计算出波达方向γ。对于宽带信号,其信号能量分布在一定范围的频带上,故在上式中对应的某些行上存在信号功率分量,这样就可以把各行在γ方向上进行信号功率积累,从而提高对宽带信号波达方向检测的性能。为了将各子带作FFT后在γ方向上信号功率实现相加积累,必须保证上式中矩阵同一列元素对应γ角度要一致,即在γ域上对齐。通过空间域插值实现。把每个子带对齐的对应各点取模平方求和,达到信号功率非相参积累的效果。
由上可得非等距线阵宽带信号处理流程:
(1)对接收信号进行时域FFT
(2)对第一步结果第一行前后两部分按欠采样率补0后分别进行相应点数FFT;
(3)对第一步结果第i(i≥2)行前后两部分补0后分别进行相应点数FFT;
(4)前后两部分对齐后分别进行功率积累;
(5)前后两部分相加进行解模糊。
原理图如图8所示。
