（1.广州大学机械与电气工程学院，广东 广州 510006；2.广东工业大学智能检测与制造物联教育部重点实验室，广东 广州 510006；3.广东工业大学物联网智能信息处理与系统集成教育部重点实验室，广东 广州 510006）

0 引言

盲源分离，又称盲信号分离，是指仅根据接收的混叠信号（观测信号）分离或恢复未知源信号，目的是求得源信号的最佳估计[1-2]。其因强大的分离功能已在通信信号处理[3]、生物医学信号处理（心肺音信号分离等）[4]、图像处理[5]以及语音信号处理[6-7]等多领域得到了广泛的应用。在实际的信号接收过程中，传感器的数目往往小于源信号的数目（即欠定混叠），导致通道的盲辨识极具挑战性，特别是在高混响复杂环境下，可听回声对音质有着重要的影响，导致接收信号具有复杂性，给源信号的分离带来了巨大的挑战，传统的盲源分离算法无法彻底解决该类问题。

对人类听觉系统特性的研究表明，当回声低于由直接声音引起的掩蔽极限时，将听不到回声，这就是人类听觉系统的时间掩蔽效应[8-9]。当回声刚好低于掩蔽极限时人类听觉系统是听不见的，人类听觉系统对那些超过掩蔽极限的回声非常敏感。在低混响环境下，可利用空间脉冲响应重塑技术完全消除可听回声，而不影响声音的质量。然而，在高混响环境下，可听回声的存在是不可避免的，对此，一些改进的空间脉冲响应重塑技术被提出[10-11]。其中，Jungmann 等[10]结合声学多输入多输出信道串扰消除和空间脉冲响应重塑技术降低了混响的影响。Mertins 等[11]提出的基于凸正则化技术实现了空间脉冲响应重塑和串扰消除。然而，以上研究主要集中于空间脉冲响应重塑技术本身，而基于该技术的盲源分离研究尚不多见。鉴于此，本文在盲源分离算法中引入空间脉冲响应重塑技术，通过改进该技术以及设计新的盲源分离算法，提出面向高混响复杂环境的欠定卷积盲源分离算法。

目前，比较流行的盲源分离算法主要利用短时傅里叶变化把时域混叠信号转换到频域中，根据信号在频域上的统计特性[12]、独立性[13]、非负性[14]、稀疏性[15]等性质，设计相应的时频域盲源分离算法。在模型变换过程中，把时域上的卷积混叠变换成频域上的瞬时线性混叠，减少了时域卷积计算带来的复杂性。在低混响混叠环境下，该模型变换具有较低的近似误差，由此衍生出一系列欠定卷积盲源分离算法[16-19]。其中，文献[16-17]基于联合矩阵块对角化方法，实现了卷积混叠信号的盲源分离；文献[18-19]基于矩阵状态协方差模型，提出了迭代期望最大化算法估计模型参数，通过实时更新优化模型参数，再用维纳滤波法分离源信号。然而，这类算法收敛速度受限，而且对通道阶数与算法初始化较敏感。

非负矩阵分解是一种机器学习算法框架，将非负矩阵分解为2 个低秩非负因子矩阵的乘积[20]，在处理卷积混叠盲源分离问题中，通过将源信号的功率谱密度矩阵分解为2 个非负矩阵的乘积，一系列基于非负矩阵分解源模型的盲源分离算法被提出[21-23]。其中，Sawada 等[21]基于非负矩阵分解的低秩源模型，利用多元复高斯分布的统计模型定义多通道欧几里得距离和多通道IS（Itakura-Saito）散度，为了最小化这种散度，通过设计适当的辅助函数，推导出乘法更新形式的优化算法；Sekiguchi 等[22]假设源图像遵循无约束全秩空间协方差矩阵的多元复高斯分布，将空间协方差矩阵限制为以频率方式联合对角化满秩矩阵，从而实现了快速多通道非负矩阵分解；Wang 等[23]通过最小体积先验分布来增强源模型的可识别性，利用最小体积正则化多通道非负矩阵分解，最大化分离源的后验分布，保证了收敛的稳定性。

然而，基于非负矩阵分解设计的优化算法对模型参数的初始化比较敏感，限制了算法的自适应性。另外，时域上的卷积混叠模型通过短时傅里叶变换变换到频域上的瞬时线性混叠模型是一种近似变换模型，其成立的前提条件是短时傅里叶变换的窗长度远大于脉冲响应的长度，而在高混响环境下该条件是很难得到满足的，极易导致较大的模型近似误差，所以在此变换模型下设计的算法往往不适用于高混响环境。对此，文献[24-25]提出基于卷积传递函数的卷积窄带近似，该卷积宽带近似模型能避免以上条件的限制，更精准地近似时域上的卷积模型，适用于高混响混叠情形，但其是卷积计算，容易带来更高的计算量。

鉴于目前研究现状，面向高混响环境的欠定卷积盲源分离问题仍然存在以下难点。

1) 在高混响复杂环境下，可听回声和混响对音质有着重要的影响，导致接收信号具有复杂性。

2) 缺乏对高混响环境下欠定卷积混叠信号精确的数学建模，导致模型近似误差增大。

3) 欠定卷积混叠盲源分离实质上是一个非线性问题，其求解困难，由于外界环境的复杂性，导致传统盲源分离算法的性能受限。

针对以上问题，本文从空间脉冲响应重塑的角度出发，结合欠定卷积盲源分离研究思路，提出一种面向高混响环境的欠定卷积盲源分离算法——全局脉冲响应欠定盲源分离（GIR-UBSS,global impulse response underdetermined blind source separation）。本文创新点概括如下。

1) 设计了全局脉冲响应网络，通过优化可调滤波器削弱可听回声的影响，提高了信号的质量。

2) 构建了面向高混响复杂环境的时频域混叠信号数学模型，降低了模型近似误差，对高混响环境具有较好的自适应性。

3) 提出了一种GIR-UBSS 算法，设计了新模型下参数的实时更新规则，实现了源信号的盲分离。理论分析与一系列仿真实验验证了GIR-UBSS 算法的有效性与优越性。

1 问题描述

对高混响环境下记录的混叠信号进行如下数学建模。

其中，xj(t)是第j个通道记录的混叠信号，时间t是连续的，i= 1,2,…,I是源信号数目，j= 1,2,…,J是传感器数目，a ji(t)是第i个源信号到第j个通道过程中产生的空间脉冲响应，si(t)是第i个源信号,τ是时延，L是脉冲响应的长度，b(t)是噪声。利用矩阵向量的形式，式(1)可表示为

其中，*是卷积符号，x(t) =[x1(t),…,x J(t)]T，是混叠系统。本文考虑高混响环境下的欠定卷积混叠盲源分离问题，即I＞J为欠定混叠，且空间混响时间逐渐增大导致高混响。盲源分离的目的是仅根据接收的混叠信号x(t)分离源信号s(t)。

2 本文算法

2.1 全局脉冲响应网络的设计

在高混响环境下，接收到的混叠信号常常伴随混响回声，为了消除或削弱可听回声的影响，本文设计一种全局脉冲响应网络，如图1 所示，该网络设计思路来源于信道串扰消除和空间脉冲响应重塑技术[10]。

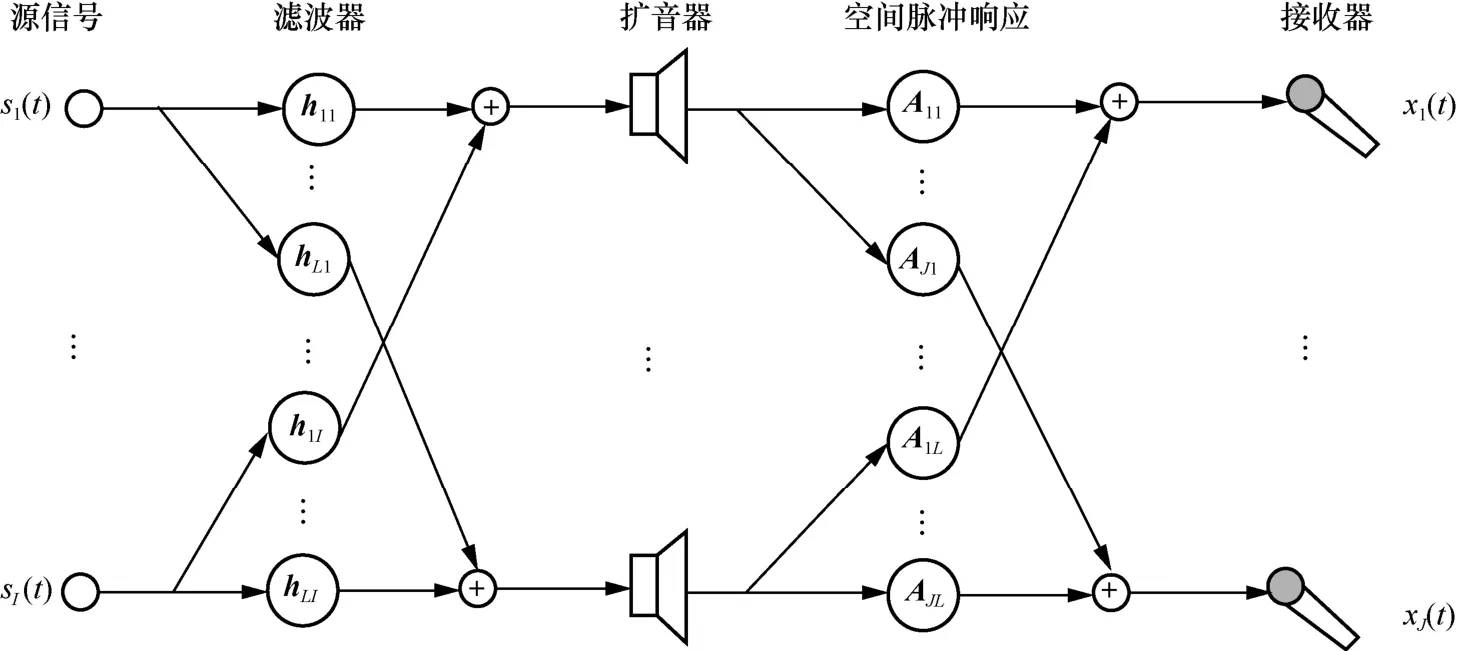
图1 全局脉冲响应网络的设计流程

考虑在接收器前安装L个扩音器，其中，I个源信号经过L个扩音器传递到J个接收器，hli是第i个源信号通过第l个扩音器产生的脉冲响应，其长度为Lh，Ajl是第l个扩音器到达第j个接收器产生的空间脉冲响应，长度为La，则从第i个源信号到达第j个接收器产生的全局脉冲响应可以表示为

其 中，N1=t0fs，N2=αfs，N3=Lg-N1-N2，n=0,…,N3-1；α和β是可调参数，在设计滤波器过程中，通过调节其值得到不同的窗函数，实现不同的滤波目的。

最小化不期望部分同时最大化期望部分，考虑优化问题

其中，pu和pd是可调的正整数，通过调节其值设计不同范数的算法，实现不同的脉冲响应重塑效果。

利用梯度下降法对式(11)求偏导，得到

2.2 欠定卷积盲源分离算法的设计

2.2.1 模型变换

为解决模型式(2)下的盲源分离问题，传统的方法利用短时傅里叶变换得到频域上近似的线性混叠模型，表示为

其中，f=1,…,F是频点指数，F是短时傅里叶变换的窗长度，n=1,…,N是时间窗指数，和分别是x(t)、s(t)和b(t)通过短时傅里叶变换得到的，噪声b(t)是模拟现实生活中的真实噪声，是频域上的脉冲响应混叠矩阵。然而，这种变换成立的前提条件是短时傅里叶变换的窗长度F远大于脉冲响应的长度L，即F≫L。在高混响环境下，随着混响时间（RT,reverberation time）的增加，脉冲响应的长度L逐渐变大，甚至超过窗长度F，导致线性混叠模型式(16)近似误差增大，甚至无效。为了避免这种限制，本文设计全局脉冲响应网络，消除或削弱可听回声的影响，缩短脉冲响应的长度，降低高混响环境的影响，建立如下近似模型。

2.2.2 非负矩阵分解模型

假设[18]

2.2.3 模型参数的更新规则

为了更好地分析，通过式(34)和式(35)表示边际分布和成对联合后验分布，即

因此，通过上述计算g和c的后验统计量，可最大化对数似然，表示为

2.2.4 频域源信号的估计

通过实时更新模型参数，得到频域上的源信号表达式为

综上，通过式(46)获得频域上的源信号，再利用短时傅里叶逆变换得到时域上的源信号，实现盲源分离。

3 实验

3.1 实验参数设置与评价准则

为了模拟真实环境，利用国际上公用的模拟环境方法[26]，创建一个有限脉冲响应房间，该房间的维数是5m×3m×2.5m，固定2 个传感器，其坐标分别为[3 1 1.6]和[3 1.05 1.6]，把源信号放置在3 个位置[2 0.5 1.6]、[2 1 1.6]和[2 1.5 1.6]，即3 个源信号两通道的欠定混叠（I= 2,J=3）。RT 设置为100～900 ms，值越大说明混响程度越强，通过此模拟环境产生有混响的欠定混叠信号。在参数设置方面，全局脉冲响应网络中La=Lh=fsRT（fs为信号的采样频率），α= 0.05，β=2.0，pu=10,pd=20，iter=1000，μ= 10-6。在非负矩阵分解源模型中，设置κi= 20；在参数初始化方面，=I，ufk和vkn利用KL（Kullback-Leibler）散度的非负矩阵分解获得，且。

为了评价GIR-UBSS 算法的有效性，利用国际公认的评价准则：信号失真比（SDR,source-todistortion ratio）、信号干扰比（SIR,source-tointerference ratio ）、信号伪像比（SAR,source-to-artifacts ratio）[27]，其值越大，盲源分离性能就越好。因此，利用评价准则SDR、SIR、SAR值的大小衡量盲源分离的好坏。

为了评价GIR-UBSS 算法的优越性，对比目前国际上比较流行的几种盲源分离算法：变分期望最大化（VEM,variational expectation-maximization）算法[19]、卷积近端交替线性化最小化（C-PALM,convolutive proximal alternating linearized minimization）算法[24]、带正则化的窄带优化（N-Regu,narrowband optimization with regularizatio）算法[24]、全秩空间协方差模型（FullRankSCM,full-rank spatial covariance model）算法[18]。其中，VEM 算法先利用卡尔曼平滑器估计混叠矩阵和源信号参数，再用维纳滤波法分离源信号。C-PALM 算法是一种卷积近似交替线性化极小化方法，通过利用卷积窄带近似获得更好的模型近似，减少了卷积核的长度，避免了短时傅里叶变换窗函数长度的限制。N-Regu 算法是一种经典的带正则化的窄带优化方法，利用了传统的线性窄带近似及1-范数正则化。FullRankSCM 算法利用满秩空间协方差模型，是EM 算法中比较成熟的方法之一。以上对比算法是解决欠定卷积混叠盲分离问题中比较流行的算法，通过与这些流行的盲源分离算法进行对比，可以很好地说明GIR-UBSS 算法的优越性。同时，所有对比算法中的参数及模型采用的是与本文实验相同的设置，这样对比更有说服力。

3.2 全局脉冲网络去混响效果分析

为了定量描述全局脉冲网络实现的去混响效果，将可感知混响量化（nPRQ,perceivable reverberation quantization）度量作为评价准则[11]，当脉冲响应被完全重塑或没有时间系数超过时间掩蔽极限时，nPRQ=0，说明混响被完全消除；否则，nPRQ 越大，脉冲响应被重塑的效果越差。为了验证全局脉冲网络对不同混响的影响，设定混响时间RT 为100～900 ms，并与原始脉冲网络进行对比，实验结果如图2 所示。相比于原始脉冲网络，在低混响下，全局脉冲网络可以完全消除混响，使nPRQ趋于0；在高混响下，全局脉冲网络可以削弱混响的影响，提高信号的质量。

图2 全局脉冲网络去混响效果

3.3 仿真实验1：英文语音信号欠定卷积盲源分离

为了验证GIR-UBSS 算法的有效性和优越性，首选3 组英文语音信号，如表1 所示。数据集来源于国际上公开的信号分离评价实验数据。本文创建一个两通道三语音源的欠定卷积混叠，利用GIR-UBSS 算法进行分离，同时与几种比较流行的盲源分离算法进行对比，实验结果如图3 所示。从图3 可知，随着RT 的增加，算法的分离性能下降，这是由于RT 的增加带来了混响的复杂性，导致分离越来越困难，其中，SDR 和SAR 的数值下降比较明显，但是SIR 的值比较稳定，这是由于本文所设计的全局脉冲响应网络可以很好地减弱RT 的影响，从而得到稳定的SIR。

表1 仿真实验1：3 组英文语音

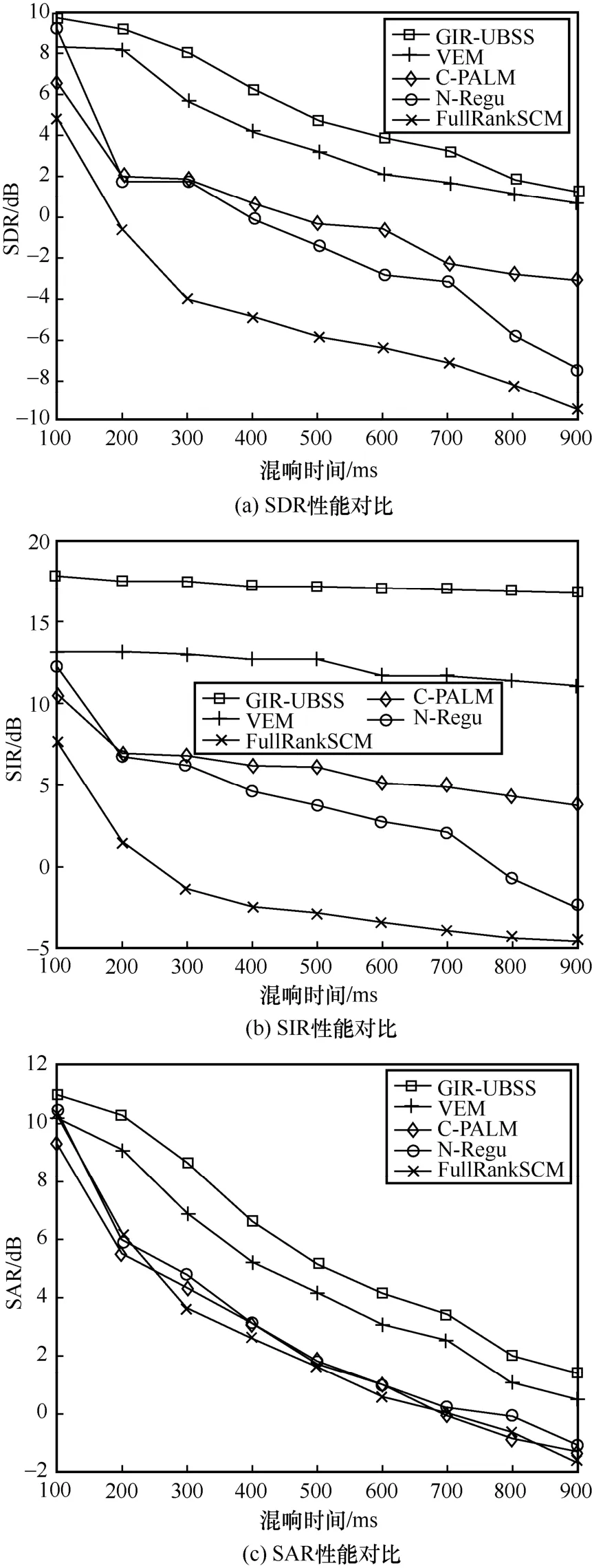
图3 英文语音信号欠定卷积盲源分离性能对比

在高混响环境下，对比算法分离性能下降严重，甚至失效，而GIR-UBSS 算法依然可获得较好的分离结果。与对比算法中最好的分离结果相比，GIR-UBSS 算法得到的SDR、SIR 和SAR 值分别提高了约1 dB、5 dB 和1 dB，该实验验证了GIR-UBSS算法在高混响环境下分离欠定卷积语音混叠信号的有效性和优越性。

另外，为了从视觉的角度解析英文语音混叠信号分离情况，可视化混响时间为300 ms 下的原始英文语音混叠信号波形以及分离后的英文语音信号波形，如图4 所示。

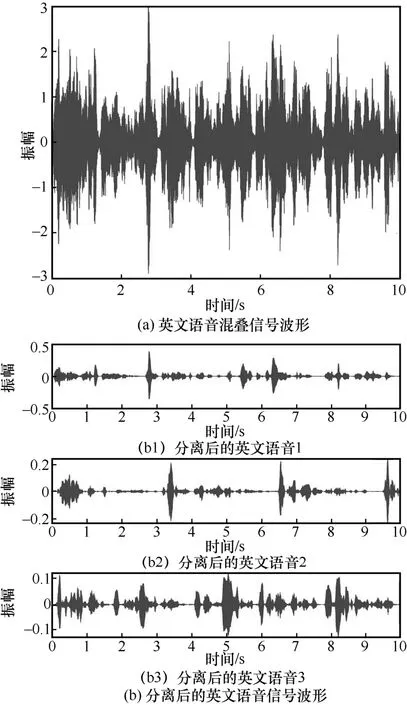
图4 英文语音混叠信号波形以及分离后的英文语音信号波形

3.4 仿真实验2：音乐信号欠定卷积盲源分离

为了验证GIR-UBSS 算法对音乐混叠信号的有效性和优越性，测试3 组音乐欠定卷积混叠信号，选取的源信号如表2 所示，该音乐信号包括吉他声、人声和鼓声，全时长为25 s，采样频率为44.1 kHz，为了减少分离所需的时间，本文实验将信号截断为10 s，下采样至16 kHz，保持与实验1 的一致性，盲源分离结果如图5 所示。

表2 仿真实验2：3 组音乐信号

图5 音乐信号欠定卷积盲源分离性能对比

从图5 可知，随着RT 的增大，算法的分离性能与预期基本一致。与对比算法中最好的分离结果相比，GIR-UBSS 算法得到的SDR、SIR、SAR 值分别提高了约6 dB、7 dB 和6 dB。该实验验证了GIR-UBSS 算法在高混响环境下分离欠定卷积音乐混叠信号的有效性和优越性。

与仿真实验1 的结果对比可发现，GIR-UBSS算法在分离音乐混叠信号表现出更好的优越性。这是由于本文利用了非负矩阵分解源模型，相比于语音源，音乐源可以被较小数目的源成分表示，更适用于非负矩阵分解模型，从而获得更好的分离结果。

为了从视觉的角度解析音乐混叠信号分离情况，可视化300 ms 下的原始音乐混叠信号波形以及分离后的音乐信号波形，如图6 所示。

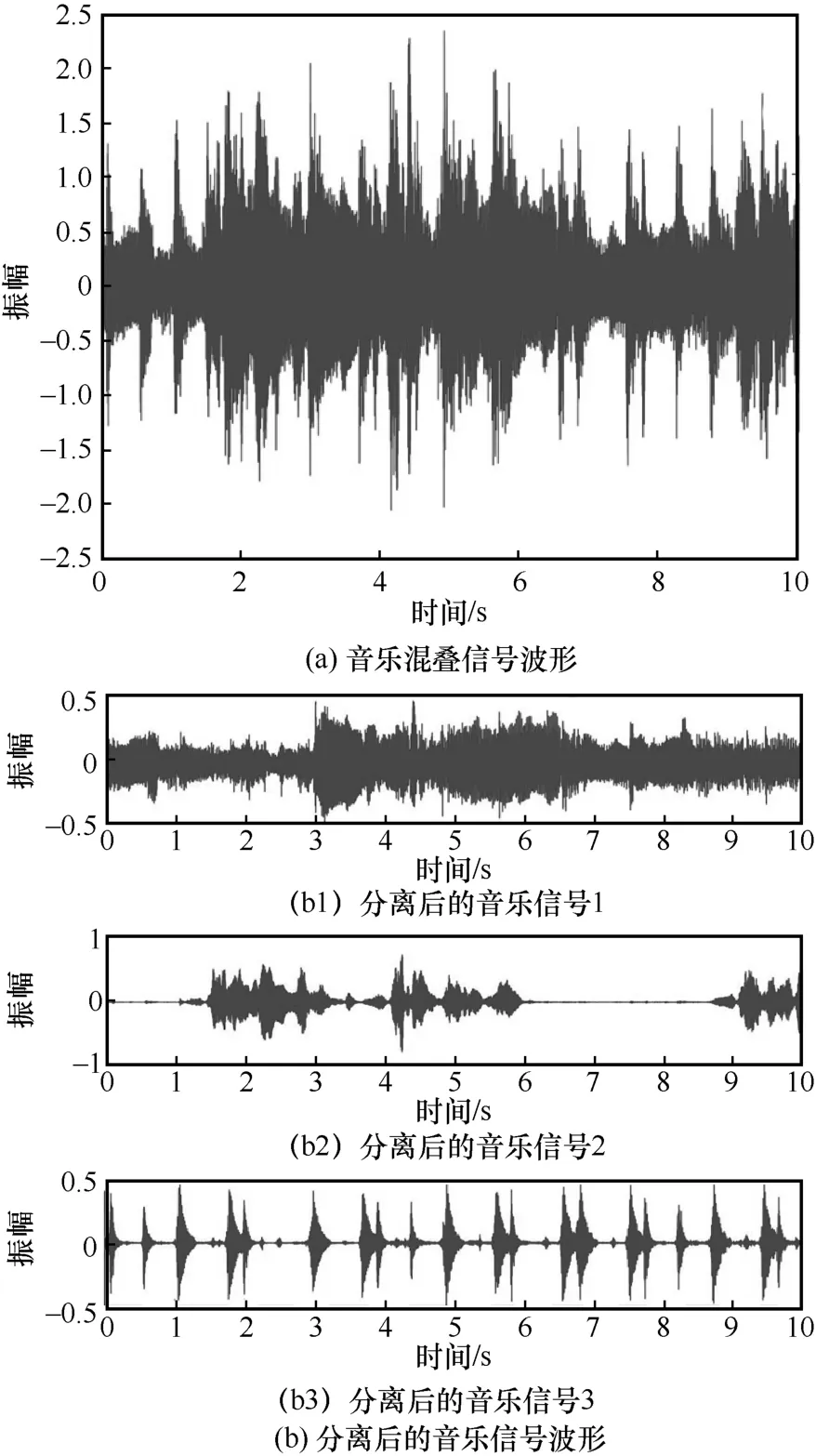
图6 音乐混叠信号波形以及分离后的音乐信号波形

3.5 仿真实验3：中文语音信号欠定卷积盲源分离

为了验证GIR-UBSS 算法对中文语音混叠信号的有效性和优越性，测试3 组中文语音混叠信号，数据集来自国内公共中文语音数据集。选取3 组语音信号，如表3 所示，盲源分离结果如图7 所示。与对比算法中最好的分离结果相比，GIR-UBSS 算法得到的SDR、SIR、SAR 值分别提高了约1 dB、5 dB 和1 dB。验证了GIR-UBSS 算法对分离中文语音欠定卷积混叠信号仍然具有较好的有效性和优越性。

表3 仿真实验3：3 组中文语音

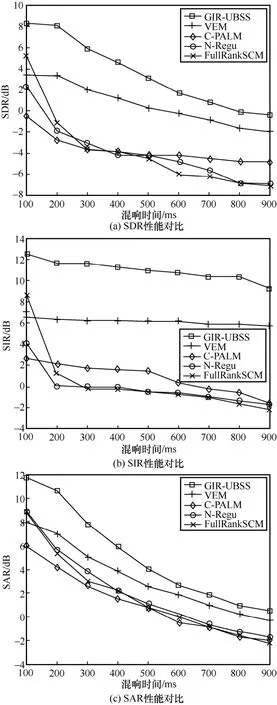
图7 中文语音信号欠定卷积盲源分离性能对比

另外，为了从视觉的角度解析中文语音混叠信号分离情况，可视化混响时间为300 ms 下的原始中文语音混叠信号波形以及分离后的中文语音信号波形如图8 所示。

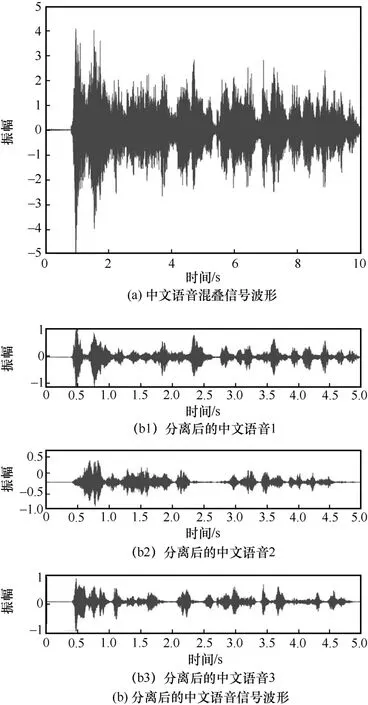
图8 中文语音混叠信号波形以及分离后的中文语音信号波形

3.6 算法对真实噪声的稳健性分析

为了验证GIR-UBSS 算法对真实噪声的稳健性，现实生活中遇到的噪声场通常可以近似为球形或圆柱形噪声场，如时间相关噪声、由相互独立的语音片段混合而成的巴布语音或工厂噪声，以及室外测量经常受到各种声源（如交通、自然环境声音等）的干扰。本文实验测试3 种真实噪声：由球形产生的各向同性噪声（isotropic noise）、由相互独立的语音片段混合而成的巴布语音噪声（babble noise）以及风噪声（wind noise）。然后分别把这3 种噪声加入仿真实验1 中的混叠语音信号中构成含噪声的混叠信号，利用GIR-UBSS 算法对混叠信号进行分离，同时对比无噪声（without noise）下的盲源分离，实验结果如图9 所示。从图9可知，加入不同噪声以后获得的盲源分离结果与无噪声下得到的结果相似，验证了GIR-UBSS 算法对真实噪声具有很好的稳健性。

图9 含有真实噪声的盲源分离性能对比

4 结束语

现实生活中，接收的混叠信号往往伴随高混响等不确定因素，如何消除或削弱高混响的影响，提高盲源分离性能，已经成为信号处理中极具挑战性和现实意义的课题。为此，本文提出一种面向高混响复杂环境的欠定卷积盲源分离算法，通过设计全局脉冲响应网络，减少脉冲响应的长度，削弱可听混响回声的影响。进而构建高混响环境的时频域混叠信号数学模型，设计新模型下的参数更新规则，实现源信号的盲分离。理论分析表明，在新的实时模型更新规则下，可得到频域上的源信号。实验验证了所提GIR-UBSS 算法对分离中英文语音混叠信号、音乐混叠信号具有很好的有效性。另外，通过与国际上比较流行的盲源分离算法对比，证实了GIR-UBSS 算法的优越性，以及对真实噪声具有良好的稳健性。