（西安电子科技大学综合业务网理论及关键技术国家重点实验室，陕西 西安 710071）

0 引言

受空间调制（SM,spatial modulation）思想启发，基于索引调制的正交频分复用（OFDM-IM,orthogonal frequency division multiplexing with index modulation）通过在正交频分复用（OFDM,orthogonal frequency division multiplexing）系统中增加子载波索引传输信息，可以在系统性能和频谱效率（SE,spectral efficiency）之间实现折中，降低了系统能量消耗[1-5]，引起了人们极大关注。

近年来，许多学者在提高OFDM-IM 的SE和误码率（BER,bit error rate）性能方面做了大量工作。文献[6-8]提出的基于联合子块索引调制的正交频分复用（OFDM-IM-JS）技术通过将多个子块的索引组合成联合索引信息改进OFDM-IM的SE。文献[9]提出的双模索引调制辅助正交频分复用（DM-OFDM）技术将每个OFDM 子块中的子载波分为两组，每组由一对可区分的映射器调制，通过牺牲能量效率可提高SE。文献[10]提出的基于索引调制的零填充三模正交频分复用（ZTM-OFDM-IM）技术将其子载波细分为若干个子块，在每个子块内，只有一部分子载波由2 个可区分的星座调制，其余保持空载，从而降低能量消耗。文献[11]提出的基于多星座选择的双模索引调制辅助正交频分复用（DM-OFDMIM-MCC）技术通过增加索引比特与符号比特的比率提高了SE。由于OFDM-IM 方案中子载波激活模式（SAP,subcarrier activation pattern）的理论总数与二进制数不匹配，上述方案均存在SAP 丢失问题，从而导致OFDM-IM 的SE 受限，并且低复杂度对数似然比（LLR,log-likelihood ratio）检测算法下的BER 性能较差[5]。针对这一问题，文献[12]提出了低复杂度的基于索引调制的正交频分复用（LC-OFDM-IM）技术，使用了所有可能的SAP 来传送数据，但它仅适用于高阶调制系统。

针对上述问题，本文提出了一种基于子载波补给索引调制的正交频分复用（OFDM-SSIM,orthogonal frequency division multiplexing with subcarrier supply index modulation）传输方案。通过补给索引，涵盖了所有理论上可能的SAP，而且与二进制数匹配。因此，该方案不仅增加了子块传输的索引信息，提高了SE，还保持了良好的BER 性能。

1 OFDM-SSIM 信号模型

1.1 发射端和接收端的信号模型

图1 给出了OFDM-SSIM 的发射端和接收端的信号模型。在发射端，输入比特由比特分流器拆分为G个子块，每个子块由pbit 组成。每组pbit被映射到一个长度为n的 OFDM 子块，其中，N是OFDM 子载波的数量。每个子块的pbit 进一步可细分为p1bit 和p2bit。输入序列的前p1bit 由补给索引调制，确定从n个可用子载波中选择的k个激活子载波。其中，i={i1,i2,…,ik}(iβ= 1,2,…,n,β= 1,2,…,k)表示选择的子载波。输入序列的后p2bit 经过M元映射器进行调制，输出的调制符号向量用s={s1,s2,…,sk}表示。然后，信号通过OFDM 复用将s上的星座点符号加载到i所对应的激活子载波上，创建所有子块，并形成长度为N的OFDM 块XF。接下来，信号进行与传统OFDM 信号相同的处理步骤，对OFDM块中的数据进行快速傅里叶逆变换（IFFT,inverse fast Fourier transform）。在IFFT 的输出端，添加长度为LCP的循环前缀（CP,cyclic prefix），然后经过并串（P/S,parallel-serial）转换和数模转换后送入信道。

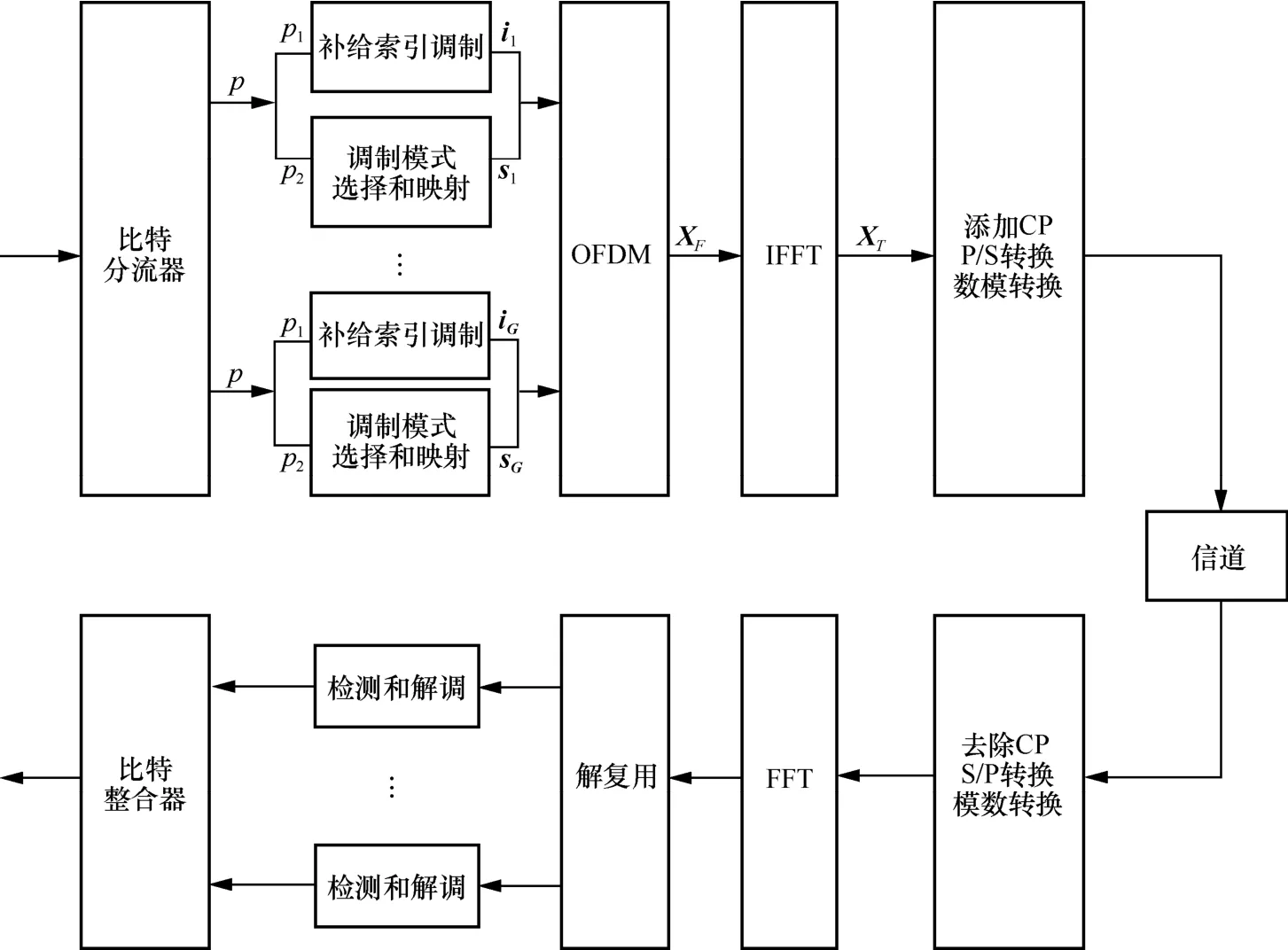
图1 OFDM-SSIM 的发射端和接收端的信号模型

在接收端，信号首先经过模数转换和串并（S/P,serial-parallel）转换去除CP。然后进行快速傅里叶变换（FFT,fast Fourier transform）和解复用，以便以子块的形式进行检测和解调。对非零子载波进行解调后，将G个OFDM 子块合并，输出信息流。

1.2 补给索引调制和符号映射

在OFDM-SSIM 的补给索引调制和符号映射过程中，pbit 信息分为索引信息p1bit 和符号信息p2bit。p1bit 信息进行补给索引调制，p2bit 信息执行符号映射。由于添加了补给索引，可以得到，其中，是向上取整。将p1bit 序列表示的二进制数设为B。如图2 所示，如果B＜，前p1bit 由原始索引映射器调制得到向量i，而后p2bit 由映射器M1调制得到向量s；如果B≥，前p1bit 由补给索引映射器调制得到向量i，而后p2bit 由映射器M2调制得到向量s。假设M1和M2调制阶数相同，并尽量选择2 个星座图的星座点之间平均距离大的映射。因此符号信息比特p2=klbM，其中，M是M1和M2的调制阶数。

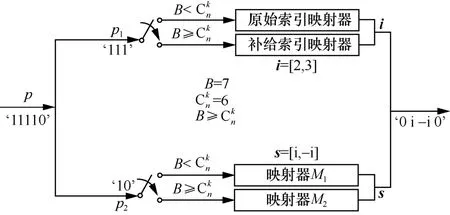
图2 OFDM-SSIM 的补给索引调制和符号映射

以采用BPSK调制且n=4、k= 2的OFDM-SSIM 方案为例。表1 给出了p1bit 索引信息流对应的SAP 和索引模式以及p2bit 符号信息流对应的映射模式。对于每个子块，p1=l bC(4,2)=3和p2= 2lb2=2，同时M1和M2分别设置为{-1,1}和{-i,i}。如图2 所示，当输入信息比特为‘11110’时，前三位为索引信息比特‘111’，即B=7，对应补给索引模式向量i=[2,3]。最后两位是信息比特‘10’，通过M2模式调制为s=[i,-i]，因此经过补给索引选择、调制方式选择和映射后，输出为‘0 i-i0’。

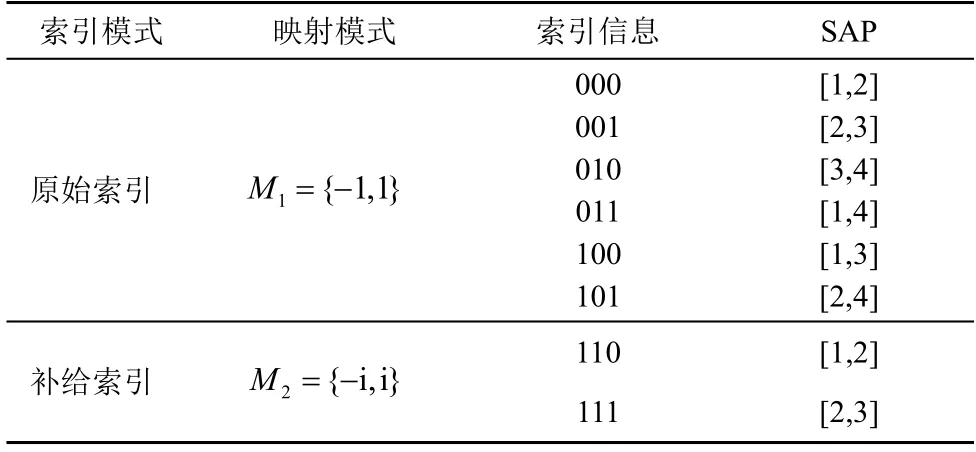
表1 n=4、k=2的OFDM-SSIM 映射信息

1.3 两级LLR 检测

由于本文方案中激活载波数目固定，并且系统SAP 全为合法SAP，因此在接收端可以采用低复杂度LLR 检测算法。

以子块为单位，计算各载波对应的对数似然比[5]为

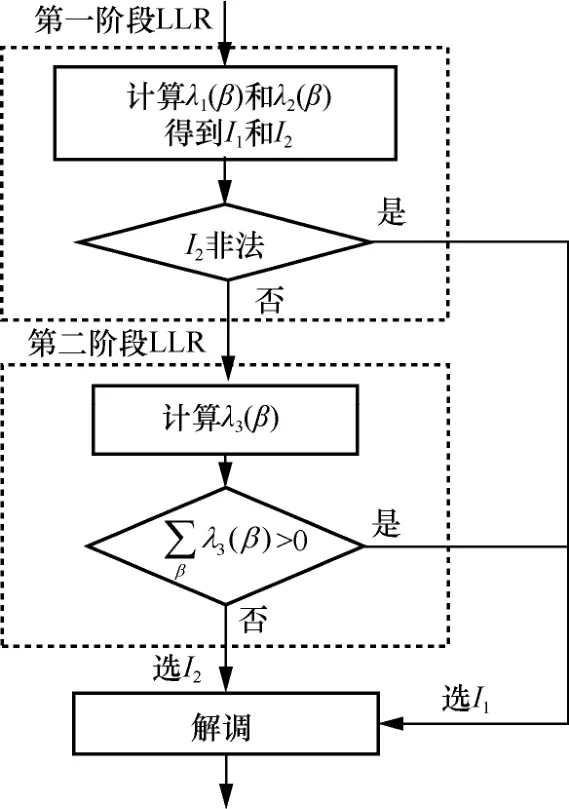
图3 OFDM-SSIM 的LLR 检测算法流程

1) 第一阶段

每个子块内的每个子载波是非空事件还是空事件的后验概率分别为

其中，Xβ(β= 1,2,…,n)是在每个子块中的n个子载波上调制的符号，S1,i和S2,j是M1和M2的第i个和第j个元素。这意味着λ1(β)或λ2(β)值越大，它们对应的子载波符号越有可能被M1或M2调制。对于每个子块，原始索引集I1和补给索引集I2分别由前k个最大的λ1(β)或λ2(β)对应子载波的位置信息决定。

为了避免采用 LLR 检测时出现类似于在OFDM-IM 方案中的错误，这里判断I2集合是否为非法索引集合。以表1 所示的情况为例，如果I2为[1,2]或[2,3]，则认为该集合合法；如果I2是其他集合，则认为该集合非法。如果该阶段检测到I2为非法位置索引，则直接解调I1对应的子载波符号；否则，I1和I2被联合输入第二阶段的LLR 检测。

2) 第二阶段

子载波被M1或M2调制的后验概率为

根据贝叶斯公式，式(4)可以进一步表示为

如果每个子块的λ3(β)值之和大于0，则将SAP检测为I1，并根据M1解调相应的子载波符号；反之，则将SAP 检测为I2，并根据M2解调相应的子载波符号。

下面比较本文方案与ZTM-OFDM-IM 方案每个子块检测中涉及的复数乘法运算次数。令n为每个OFDM 子块中的子载波数，M为调制阶数。由式(1)可以看出，LLR 检测第一阶段中，2 种方案都需要对每个子块中所有子载波的所有可能的调制方式进行计算，因此复杂度相同，即需要2nM次复数乘法。LLR 检测第二阶段中，对于ZTM-OFDM-IM 方案，每个激活子载波有2 种可能的调制方式，因此复杂度为2kM；对于OFDM-SSIM方案，存在2 种情况，若第一阶段检测出的SAP 相对应的只有一种调制方式，则直接对确定的激活子载波进行解调，此时复杂度为kM；若第一阶段检测出的SAP 相对应的有2 种可能的调制方式，复杂度为 2kM（与 ZTM-OFDM-IM 方案相同），故OFDM-SSIM 方案第二阶段的平均复杂度为，其中，和分别为2 种情况出现的概率。

以采用BPSK 调制且n=4、k= 2为例，在第一阶段中，2 种方案LLR 检测均需要2nM=16 次复数乘法。在第二阶段中，对于ZTM-OFDM-IM 方案，每个激活子载波有2 种可能的调制方式，需要2kM=8 次复数乘法；对于OFDM-SSIM 方案，需要的复数乘法运算次数为，显然本文方案复杂度较低。

2 性能分析

2.1 频谱效率

假设信息源是均匀分布的，子块传输的总信息比特数与使用的子载波数之比表示系统的SE[13]，因此OFDM-SSIM 的SE 可以表示为

基于上述分析，本文方案相比OFDM-IM 在保证激活载波比例不变的情况下，增加了传输的信息，从而提高了SE 和能量效率。表2 给出了在激活子载波4 选2 的情况下，采用BPSK 调制的OFDM-SSIM、OFDM-IM 和ZTM-OFDM-IM 方案的SE。从表2 可以看出，相比传统的OFDM-IM，本文方案在SE 上有25%的提高。

表2 3 种方案的SE 比较

2.2 误码率

以BPSK 调制方式为例，OFDM-IM 和OFDMSSIM 方案的星座分布分别如图4 和图5 所示。

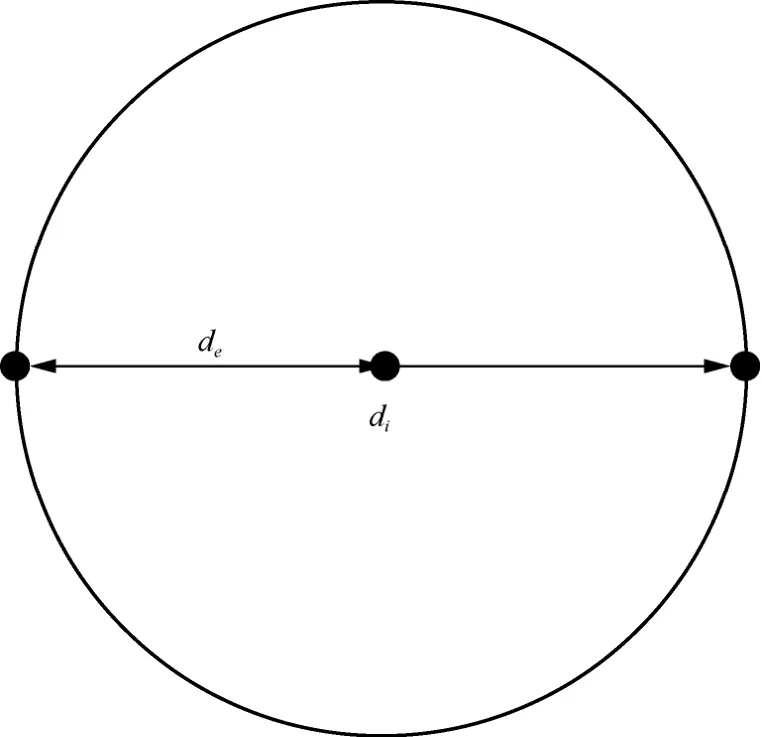
图4 OFDM-IM 方案的星座分布

在OFDM-SSIM 和OFDM-IM 方案中，由于有子载波静默，在星座图中引入了零点。在图5中，当子载波以的比率激活时，即，有一半的点落在零点附近。位于-1 和1 附近的点是所有具有原始索引模式的子块中激活子载波上的星座点，数量是所有点的。位于i 和-i 附近的点是所有具有补给索引模式的子块中激活子载波上的星座点，数量是所有点的。

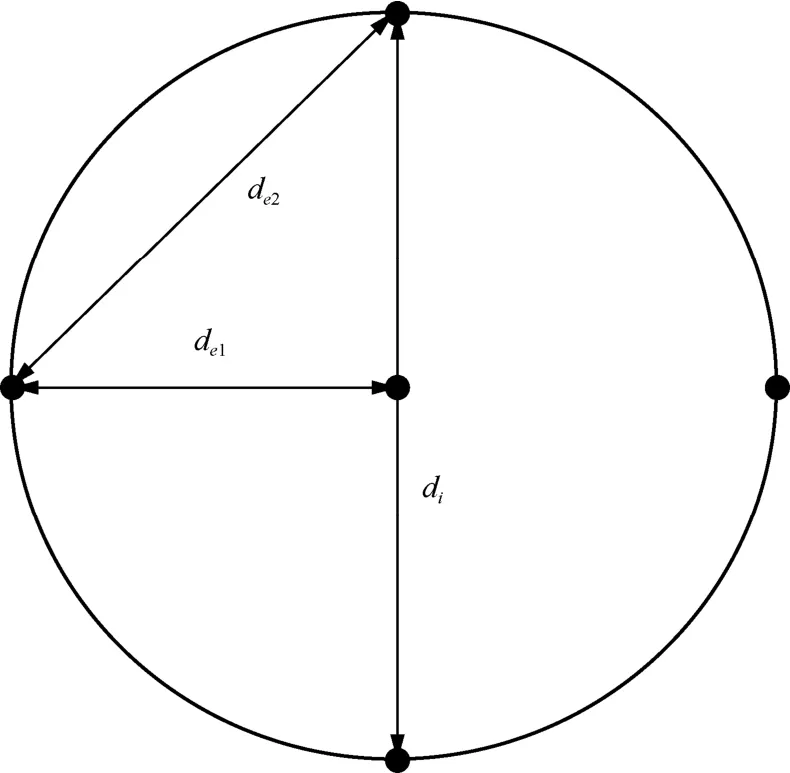
图5 OFDM-SSIM 方案的星座分布

OFDM-SSIM 和OFDM-IM 方案的BER 为[5]

其中，e(x→x')表示发送端发送向量x在接收端被错译为x'的比特数，A=(x-x′)H(x-x′)，h表示信道衰落系数。由式(7)可知，系统BER 性能由x与xˆ 之间的距离决定[14]，这一距离可以分为模式间距离与模式内距离，共有3 种错误情况，如图5 所示。第一种错误情况为将原索引模式错译为另一种原索引模式或将补给索引模式错译为另一种补给索引模式。这时，发送向量和错译向量之间的最小距离可以表示为

其中，h1和h2表示发生错译的子载波对应的信道衰落系数向量中对应的信道衰落系数。第二种错误情况为将原索引模式错译为补给索引模式或将补给索引模式错译为原索引模式。这时，发送向量和错译向量之间的最小距离可以表示为

第三种情况是索引正确，而模式内的符号错译。这种情况下两向量间距离最小，可以表示为

从而系统误码率可以近似表示为

其中，n1表示第一种错误情况的个数，pb1表示第一种情况错译的比特数；n2表示第二种错误情况的个数，pb2表示第二种情况错译的比特数；n3表示第三种错误情况的个数，pb3表示第三种情况错译的比特数；p表示OFDM-SSIM 各子块可以传输的信息比特；f(x)表示为

本文方案和OFDM-IM 相比增加了第二种错误出现的情况。在信源均匀分布的情况下，以表1中情况为例，补给索引模式出现的概率为，所以第二种错误出现次数相较于第一种和第三种错误出现次数较低，计算可得，并且由于OFDM-SSIM 方案增加了系统传输的信息比特p，当信噪比较小时，有

此时，OFDM-SSIM 方案的误码率性能与OFDM-IM 近似相同。当信噪比较大时，有

由于 OFDM-SSIM 方案传输的信息比特总数p大于OFDM-IM 方案，因此当信噪比较大时，OFDM-SSIM 方案的BER 性能优于OFDM-IM方案。

3 性能仿真

本节给出了AWGN 信道和瑞利衰落信道下，本文提出的OFDM-SSIM 与传统的OFDM-IM 和ZTM-OFDM-IM 的性能比较。

仿真中，信道路径数目为8、各径之间相隔一个采样周期、衰落系数相互独立，且服从均值为0、方差为1的复高斯分布。图6和图7中，OFDM-SSIM和 ZTM-OFDM-IM均采用M1={-1,1}和M2={-i,i}的BPSK 星座映射，OFDM-IM 采用M1={-1,1}的星座映射；图8 中，OFDM-SSIM 采用M1={-1,-i,1,i}和M2=的QPSK 的星座映射，OFDM-IM 采用M1={-1,-i,1,i}的QPSK 的星座映射。

图6 给出了OFDM-SSIM、OFDM-IM 和 ZTMOFDM-IM 在AWGN 信道和瑞利衰落信道下的吞吐量[13]，这里吞吐量定义为单位频带上每秒成功传输的比特数。从图6 可以看出，3 种方案的吞吐量在信噪比（SNR,signal-to-noise ratio）达到18 dB 以上时趋于稳定，分别达到1.25、1.00、1.25。这证明了此时的吞吐量即理论可达SE，且OFDM-SSIM 的SE 比OFDM-IM 的SE 高25 %，这与前面的理论分析相吻合。

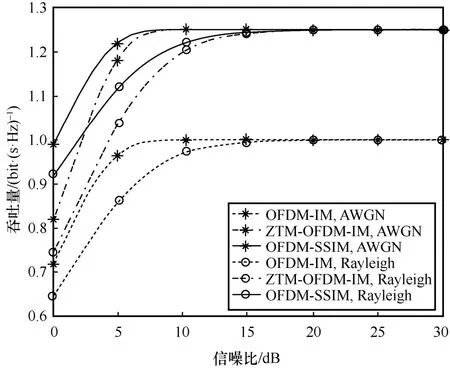
图6 AWGN 信道和瑞利衰落信道下的吞吐量

图7 给出了 OFDM-SSIM、OFDM-IM 和ZTM-OFDM-IM 在AWGN 信道和瑞利衰落信道下的误码率性能曲线。从图7 可以看出，无论在AWGN 信道下还是瑞利衰落信道下，OFDM-SSIM的性能均优于OFDM-IM 和ZTM-OFDM-IM。在AWGN 信道下，当误码率为 10-2时，OFDM-SSIM比ZTM-OFDM-IM 有约1 dB 的增益。进一步可以看出，在瑞利衰落信道下，OFDM-SSIM的误码率性能优势随着信噪比的增加而降低。这是由于在OFDM-IM 和ZTM-OFDM-IM 的检测中，实际产生的 SAP 与理论上所有可能的SAP 之间不匹配，导致错误随着信噪比的增加而减小。

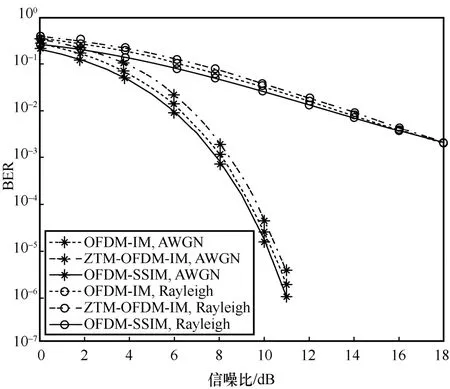
图7 AWGN 信道和瑞利衰落信道下的BER 性能

图8 给出了OFDM-SSIM 和OFDM-IM 在瑞利衰落信道下分别采用QPSK 和BPSK 调制时的BER 性能。从图8 可以看出，当频谱效率为1.25 bit/ (s·Hz)、误码率为10-2时，OFDM-SSIM 相比OFDM-IM 有约2 dB 的增益。

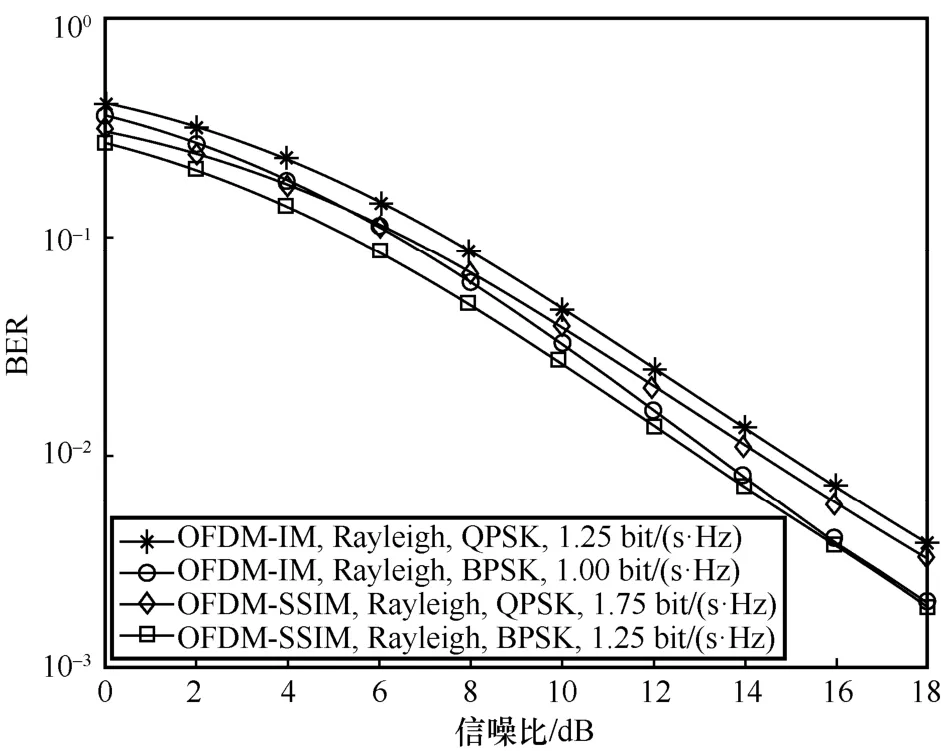
图8 瑞利衰落信道下OFDM-IM 和OFDM-SSIM在不同调制方式下的BER 性能

4 结束语

本文提出了一种新的OFDM-IM 传输方案，即OFDM-SSIM。该方案通过提高索引利用率增加了每个子块传输的信息量，提高了系统SE 性能。此外，由于本文方案的可用索引与所有可能的SAP 相匹配，使接收端使用低复杂度LLR 检测算法具有良好的BER 性能。