（北京信息科技大学信息管理学院，北京 100192）

0 引言

随着大数据、云计算、人工智能等网络信息技术的不断发展，互联网已经成为我国信息化建设的基础设施。与此同时，国家、企业和个人的网络安全也面临严峻的挑战，攻击者通过软件应用漏洞、不安全网络协议等进行网络攻击，入侵目标主机并获得高级权限，或植入病毒以获利，给国家和企业带来了难以估量的损失。因此，发现网络中潜在的安全隐患，及时采取有效的防护措施，对提高网络整体的安全性有着重要的意义。在对网络的安全性进行分析时，从攻击者的角度出发往往可以获得更全面的评估结果，攻击者从网络中的某个边界点渗透网络，利用网络和主机中的漏洞逐步转移，最终获得目标状态节点的权限。通过模拟攻击者的攻击过程，分析潜在的攻击路径，找出网络中的薄弱环节和潜在威胁并及时修复，能够有效保护国家、企业和个人的网络空间安全。

攻击图技术作为网络安全分析和评估手段，可以有效满足上述需求。攻击图以图形化的方式展示了攻击者连续的攻击行为所组成的攻击路径，构建目标网络拓扑的攻击图既可以分析攻击者的攻击路径，对该路径上的重点环节进行保护，也可以实时分析攻击者的攻击意图和动向，并及时采取防御和反制措施。由于攻击图技术在网络安全评估领域具有良好的应用前景，目前已经成为学术界和工业界的重点研究内容。

攻击图根据其顶点和边所代表的不同意义，可以划分为不同种类的攻击图，如状态攻击图[1]和属性攻击图[2]等。在状态攻击图中，顶点代表网络状态信息，边代表节点状态的迁移。Bhattacharya 等[3]使用状态搜索技术来构建目标网络的状态攻击图。然而，随着网络规模的不断扩大，网络的状态数量爆炸性增长，状态攻击图难以分析大规模网络拓扑，因此，针对状态攻击图的研究逐渐减少。为了扩大可分析网络的规模，研究人员开始研究属性攻击图。属性攻击图的顶点表示条件和漏洞，边表示漏洞利用条件，相对于状态攻击图，属性攻击图的结构简洁，生成效率更高，适合大规模的网络拓扑环境。为了解决属性攻击图中的环路问题，陈锋等[4]提出n-有效攻击路径的概念，假设无环攻击路径理论最大长度为n并提出n-有效攻击路径的发现算法。

上述研究主要集中在攻击图的构建以及复杂度的优化等方向，为后续研究提供了坚实的基础，但缺乏对网络环境中关联信息的考虑。近些年，攻击图技术更多地应用在风险评估、威胁分析及网络加固等领域。通过构建目标网络的攻击图，模拟攻击者的行为，并且结合网络配置信息及漏洞信息，分析网络中潜在的攻击路径、具有安全隐患的软件程序以及服务应用的漏洞。Kaynar 等[5]分析了攻击图的研究现状，认为当前研究的重点是攻击图的可达性分析和路径研究。杨宏宇等[6]考虑了主机节点间的关联关系对其风险值的影响，根据资产保护价值和攻击图结构计算主机的重要度，并利用节点最大路径概率及主机重要度来度量主机节点风险值，全面分析了目标网络中主机节点的风险。以上研究实现了对网络环境的静态风险评估，帮助防御者更加清晰地认知脆弱节点之间的关联，并采取相应的防护措施，及时使用补丁或更安全的服务应用来减少网络的安全风险。除了基于网络环境中的拓扑信息进行静态风险评估外，动态分析网络环境中的威胁因素也十分重要。罗智勇等[7]在预测攻击路径时，加入了攻击代价和入侵意图等影响因素，通过综合计算攻击成本、漏洞价值和攻击收益来定义攻击图中的状态转移概率，为动态评估网络风险提供了依据。王文娟等[8]提出了一种概率攻击图更新算法，通过构建动态概率攻击图模型，设计算法推断攻击意图及攻击路径，为还原针对云计算环境的渗透攻击过程提供了有价值的参考依据。Hu 等[9]提出了基于动态贝叶斯攻击图的威胁预测算法，通过实时攻击检测和多维度告警信息，评估攻击者能力并计算漏洞利用成功率，实现了对网络威胁程度以及遭受攻击风险的量化。

除了依靠关联信息分析网络安全状态外，攻击图还可以与概率论相结合。攻击图反映了网络内可能的攻击路径，判断图中哪些路径更有可能被攻击者使用是攻击图的一个重要功能。基于攻击图中状态连续变化这一特点，研究人员通过引入贝叶斯网络与马尔可夫模型来计算节点的状态转移概率。陈小军等[10]将转移概率表引入攻击图，从观测事件出发，推导出单步攻击发生的概率，提出了一种计算成功概率最高的攻击路径的方法，能够有效推断攻击意图并计算攻击路径。胡浩等[11]使用马尔可夫链（MC,Markov chain）对网络攻击中的状态迁移过程进行刻画，认为现有研究大多围绕理想攻击场景，然而实际情况中攻击者采用的攻击路径不一定是理想攻击路径，因此提出了基于吸收马尔可夫链的入侵路径预测方法，基于通用漏洞评分标准，从多种层次出发，全面感知网络中的威胁。张凯等[12]针对基于马尔可夫链的分析方法中存在的计算状态转移概率不合理等问题，提出了状态节点转移失败的计算方法，该方法得到的结果更加符合真实的网络攻防状况。Durkota 等[13]提出了一种基于攻击图的博弈模型，该模型将攻击图转换为马尔可夫决策过程，并通过修剪技术，使安全研究人员可以通过蜜罐技术提高网络的安全性。Malik 等[14]设计了一种将攻击树转换为马尔可夫决策模型的算法，对攻击场景进行建模并对其进行网络安全分析，该算法结合马尔可夫决策过程和概率模型，克服攻击树中状态爆炸的问题，实验结果表明，该算法能够显著提高网络安全分析能力。此外，考虑到漏洞生命周期[15]对网络攻击分析过程的影响，胡浩等[16]以漏洞先验历史信息为输入，构造了基于马尔可夫链的漏洞生命周期模型，在时间维度上对漏洞演化过程进行推导，对其生命周期各状态的演化规律进行了分析和总结。表1 对上述研究内容进行了划分整理。

表1 研究内容划分

梳理上述研究后发现，早期文献多使用单一攻击图分析攻击路径，但由于网络规模的不断扩大，构建攻击图的复杂度也在不断增加，并且生成的攻击图过于庞大，难以直观地供研究人员分析。文献[1,3-4]对攻击图的生成算法及路径规划进行优化，降低了攻击图生成的复杂度并简化了攻击图，对基于攻击图的入侵路径研究做出了贡献。文献[5-7]考虑了除网络基本拓扑信息外能够评估目标网络安全性的因素，可以更全面地辅助安全人员进行防御决策。文献[2,8-9]构建了基于图论的动态风险量化与评估模型，进一步完善了网络风险评估体系。文献[10-14]基于概率论将马尔可夫模型应用于攻击图中，提供了一种网络攻击分析的新思路。上述研究为网络攻击研究领域做出了巨大贡献，推动了该领域的进步，然而，这些方法仍存在一些不足，例如，基于攻击图的研究中通过安全研究人员的主观经验确定节点的状态转移概率，在计算状态转移概率时缺乏统一的标准，同时也缺乏准确性与合理性（状态转移概率依赖主观经验）；现有文献的研究内容大多基于理想的攻击场景，未考虑实际环境中漏洞的生命周期对原子攻击成功概率的影响（攻击图中状态转移概率影响因素考虑不全面）；在构建漏洞生命周期风险度量模型后，没有具体应用于真实网络场景中。针对上述研究中存在的不足，本文提出了一种基于吸收马尔可夫链攻击图的网络攻击分析方法，该方法摒弃了传统攻击图研究中概率确定的主观因素，并且充分考虑了节点上漏洞生命周期对状态转移概率的影响，从攻击路径长度、节点威胁程度、预期影响（EI,expected impact）3 个方面进行全面分析，能够为安全研究人员提供科学的指导依据。本文的主要贡献如下。

1) 针对吸收马尔可夫链攻击图中对状态转移概率影响因素考虑不全面的问题，在通用漏洞评分系统（CVSS,common vulnerability scoring system）的基础上，引入漏洞生命周期模型，并提出了基于吸收马尔可夫链攻击图的网络攻击分析方法，能够辅助安全研究人员掌控网络整体的安全状态，为进一步分析网络攻击提供理论基础。

2) 针对传统攻击图模型中状态转移概率的确定依赖主观经验的问题，设计了一种基于漏洞生命周期的状态转移概率（STPVL,state transition probability based on vulnerability life cycle）归一化度量算法，将攻击图映射为吸收马尔可夫链攻击图，为分析网络攻击提供了定量数据参考，提高了分析结果的准确性与可靠性。

3) 针对映射后的吸收马尔可夫链攻击图，提出了3 种网络攻击分析方法：攻击路径长度分析方法、节点访问频度分析方法以及预期影响分析方法，为防御人员掌握网络中潜在攻击路径、攻击开销以及各节点的重要程度提供了方法支撑。

4) 对实验网络环境进行分析验证，实验结果表明，本文方法可以有效预测节点威胁程度、攻击路径长度以及预期影响。同时，通过模拟实验统计1 000 次模拟攻击中的路径选择分布与节点威胁程度变化趋势，实验结果与本文方法分析得到的理论预期具有一致性。最后通过对比实验，将本文方法与典型方法进行比较，证明了本文方法的有效性和合理性。

1 模型设计

为了解决现有攻击图模型中状态转移概率的确定依赖主观经验的问题，以及攻击图中存在的状态转移概率影响因素考虑不全面等问题，本文提出了一种基于吸收马尔可夫链攻击图的网络攻击路径分析方法。首先，该方法在原有攻击图技术的基础上，引入吸收马尔可夫链的概念，将攻击图技术与吸收马尔可夫链相结合；其次，在CVSS 漏洞评分标准的基础上，设计了一种将普通攻击图映射为吸收马尔可夫链攻击图的算法——STPVL 归一化度量算法，该算法以攻击图为输入，以基于吸收马尔可夫链的状态转移概率矩阵为输出，将攻击图映射到吸收马尔可夫链中；最后，利用算法结束后输出的状态转移概率矩阵的相关性质，对节点威胁程度、攻击路径长度以及预期影响逐一分析，为安全研究人员提供有价值的参考信息。

本文方法摒弃了传统概率确定方法中的主观性，有效提高了计算状态转移概率的准确性，同时，考虑到现有基于攻击图技术的攻击路径研究未分析漏洞时效性因素的影响，不利于网络拓扑系统整体的动态安全性，本文将漏洞的生命周期作为计算因子融入状态转移概率的计算中，设计了基于吸收马尔可夫链攻击图的网络攻击路径分析模型，共分为3 个阶段：攻击图的生成阶段、攻击图到吸收马尔可夫链攻击图的映射阶段和网络攻击分析阶段，如图1 所示，包括以下5 个步骤。

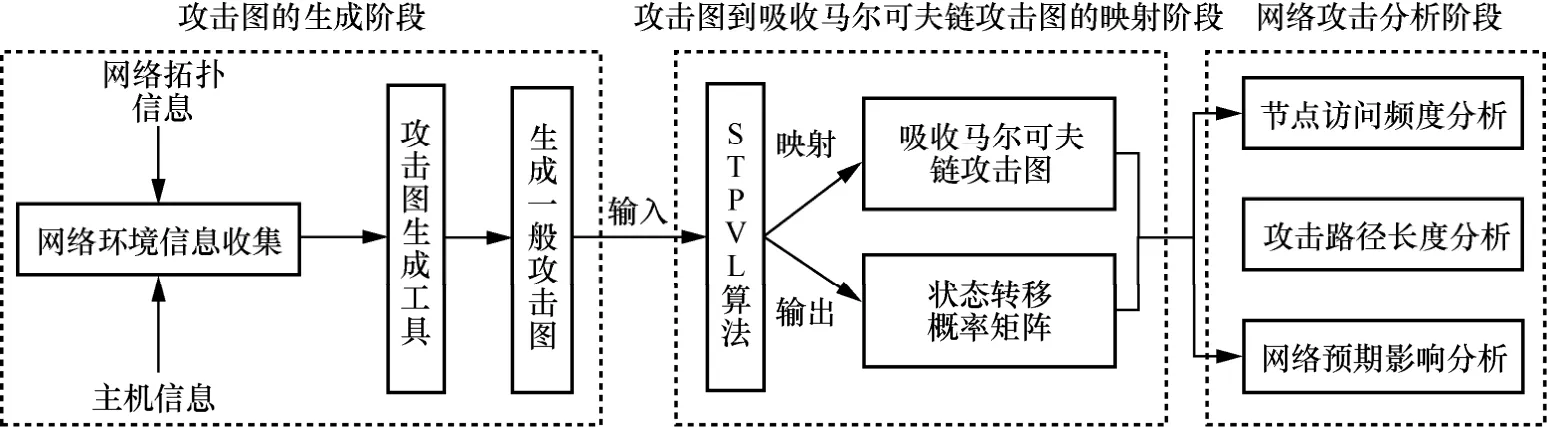
图1 本文方法模型

步骤1网络环境信息收集。使用Nessus 等漏洞扫描及IP 探测工具扫描目标网络拓扑信息、主机服务器存在的漏洞信息、网络节点的配置信息以及其他相关信息等，作为构建攻击图的要素。

步骤2一般攻击图生成。将步骤1 中收集到的网络环境信息作为输入，使用Mulval 等攻击图生成工具构建目标网络的一般攻击图。

步骤3一般攻击图到吸收马尔可夫链攻击图的映射。根据STPVL 算法将目标网络的一般攻击图重构为吸收马尔可夫链攻击图。

步骤4状态转移概率及相关矩阵的计算。通过STPVL 算法得到吸收马尔可夫链攻击图的状态转移概率矩阵P，并利用其相关性质计算节点访问频度矩阵N，攻击路径长度期望矩阵t，具体计算方法见第4 节。

步骤5网络攻击路径分析。利用得到的目标网络攻击图以及矩阵P、N、t，从攻击者的角度对网络攻击路径进行安全分析。

2 攻击图的生成

在不同类型的攻击图中，顶点可以表示主机、服务、漏洞、权限等网络安全相关要素，也可以表示权限获取等网络安全相关状态；边表示攻击者的攻击行为。攻击图技术通过构建完整的网络安全模型，能够直观地反映网络环境的脆弱性并发现潜在的攻击路径，弥补了以往技术只能通过漏洞数量与威胁等级对网络安全性进行分析，而不能根据节点在网络中的位置和功能进行评估的不足。根据攻击图中节点类型的不同，攻击图可以分为属性攻击图和状态攻击图，为合理分析和评估主机安全状况，本文选用状态攻击图从主机层面对主机进行安全评估。

2.1 定义攻击图

定义1攻击图（AG,attack graph）。AG 由四元组(S,A,V,E)构成，其中，S表示状态节点集合，A表示原子攻击集合，V表示漏洞集合，E表示状态转移的有向边集合。

1)S= {Si|i= 1,2,…,n}由n个状态节点组成，其中包括3 种不同类型的节点：初始状态节点、过渡状态节点、目标状态节点（吸收状态节点）。初始状态节点指攻击发起时的状态节点，目标状态节点指攻击结束时想要到达的状态节点，不属于以上两类的节点均为过渡状态节点。

2)A表示对漏洞的一次利用，若攻击成功，则发生节点之间的状态转移；反之，则视为状态节点到自身的一次自我访问。

3)V= {Vi|i= 1,2,…,m}，可利用漏洞Vi表示攻击图中状态跃迁过程所利用的主机漏洞或服务器漏洞，Score(Vi)表示该漏洞的可利用得分。

4)E= {Ei,j|i,j= 1,2,…,n}，Ei,j是从节点Si指向节点Sj的有向边，对应一次状态转移过程。若Ei,j存在，则表明可从状态节点Si转移至状态节点Sj。

2.2 构建攻击图

根据收集到的漏洞信息与主机通信规则构建攻击图。由于真实网络环境中主机可能存在多种漏洞，为简化攻击图规模，分析攻击者最可能的攻击意图，当多条边同时指向同一主机时，仅保留原子攻击概率最大漏洞所在的边，攻击图示例如图2 所示。对于攻击图示例中的一般攻击图（如图2(a)所示），S1～S4表示攻击者所在主机的不同状态，其中，S1为攻击者初始状态节点，S4为攻击者的目标状态节点，S2和S3均为过渡状态节点。节点之间的有向边E1,2～E3,4表示攻击图中攻击者成功利用漏洞从前置主机渗透到后置主机的过程，节点指向自身的边表示攻击失败，状态转移可以看作原状态节点到自身的一次转移。图2(b)是图2(a)所对应的马尔可夫链攻击图，其中，边上的数值表示状态转移发生的概率，其数值由状态转移概率矩阵计算得出。

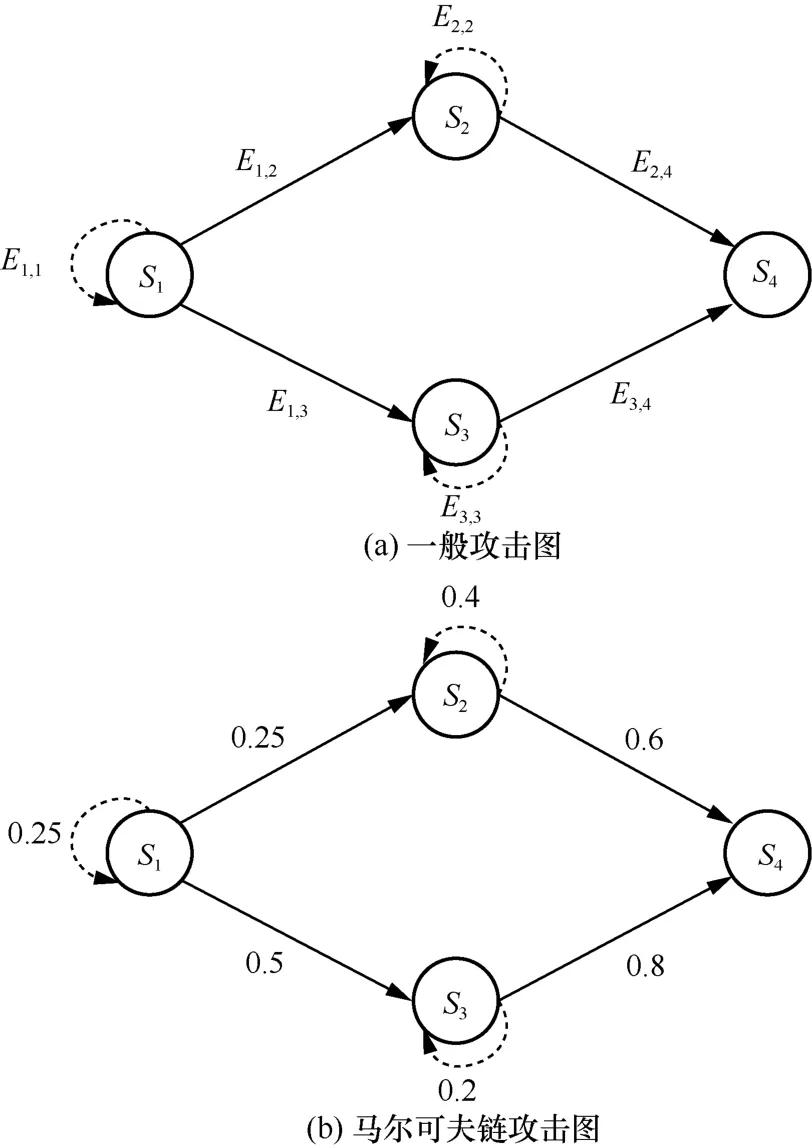
图2 攻击图示例

3 一般攻击图到吸收马尔可夫链攻击图的映射

本文基于CVSS，设计了一种将一般攻击图映射为吸收马尔可夫链攻击图的算法，该算法通过计算输入攻击图的状态转移概率矩阵，为后续网络攻击分析提供计算依据。本节将依次对吸收马尔可夫链、CVSS 漏洞评分标准以及吸收马尔可夫链攻击图的映射算法进行详细介绍。

3.1 吸收马尔可夫链

定义2马尔可夫链[17]。马尔可夫链是一个包含有限状态的随机序列集合X={X1,X2,…,XN}，其时间和状态都是离散的。马尔可夫链的无后效性使从节点Si转移至下一个节点Sj的概率Pi,j仅与当前状态有关，而与之前的状态无关，Pi,j为马尔可夫链的状态转移概率，P为由Pi,j组成的状态转移概率矩阵。

定义3吸收马尔可夫链（AMC,absorbing Markov chain）。满足以下2 个条件的马尔可夫链被称为吸收马尔可夫链：至少具有一个吸收状态，从每个状态节点都能够转移至吸收状态。吸收马尔可夫链的状态转移概率矩阵的标准形式为

其中，Q是大小为a×a的过渡状态转移概率矩阵；R是大小为a×b的矩阵，表示从过渡状态转移到吸收状态的概率；0 是大小为b×a的零矩阵；I是大小为b×b的单位矩阵；P的大小为(a+b)×(a+b)，a+b表示状态总数。

3.2 CVSS 漏洞评分标准

CVSS 是由美国国家基础建设咨询委员会委托制作、美国国家漏洞库（NVD,national vulnerability database）[18]发布的漏洞领域的公开测评标准，其评分用于表示漏洞利用的难易程度，如表2 所示。网络的安全性取决于与靶机机器上运行的服务相关的不同漏洞的可利用性等级。CVSS 定义了基本可利用得分Score(v)度量漏洞v的脆弱性，CVSS 标准提供了漏洞可利用得分的计算框架，定义如下。

定义4漏洞可利用得分（VES,vulnerability exploitability score）。CVSS 给出了漏洞可利用得分通用标准，计算式为

其中，AV、AC 和Au 分别代表漏洞的攻击向量（AV,access vector）、攻击复杂度（AC,access complex）和身份认证（Au,authentication），如表2 所示，不同漏洞的具体数值可由NVD 查询得到。Score(v)的范围为0～10，漏洞的利用难度与Score(v)成反比，即得分越高，漏洞越容易被利用；得分越低，漏洞越难被利用。例如，漏洞CVE-2014-0416 的攻击向量、攻击复杂度和身份认证分别为1.000、0.710 和0.704，通过式(2)计算该漏洞的可利用得分为10.0，表明其具有很高的可利用性。本文基于CVSS 漏洞可利用得分，度量攻击图中的状态转移概率，并提出一种STPVL 归一化度量算法，有效增强了研究的通用性。

表2 CVSS 漏洞评分标准

3.3 吸收马尔可夫链攻击图的映射算法

在攻击图中，当前状态能否向下一个状态转移只取决于当前状态是否满足漏洞利用的前置条件，而与之前的状态无关，若将攻击图中的状态节点集合当作马尔可夫链的状态空间，则状态空间的转移正好符合马尔可夫链的无后效性；攻击图中原子攻击的成功率可以作为马尔可夫链的状态转移概率；由于攻击图中必然包括目标状态节点，而攻击图的目标状态可被视为马尔可夫链中的吸收状态，因此，攻击图能够映射到吸收马尔可夫链模型，利用吸收马尔可夫链对入侵路径进行分析的理论依据成立。

在攻击图中，一次成功的原子攻击会造成一次状态的转移，然而在现实网络环境中，由于攻击者知识的储备量不同、攻防场景快速变化，目标网络环境通常处于非理想状态。在非理想状态下，一次失败的原子攻击可以视为状态节点到自身的一次转移。对于状态转移概率Pi,j的计算，本文提出了一种STPVL 归一化度量算法，将完整的攻击图转化为吸收马尔可夫链攻击图，并给出其状态转移概率矩阵P。文献[12]充分考虑了漏洞利用失败时节点到自身的状态转移概率，对包括初始状态节点在内的过渡状态节点设置到自身的转移边，综合节点所有的出度边改进了状态转移边的概率计算方法，然而其在计算节点状态转移概率时，并未考虑到漏洞生命周期对该漏洞利用成功率的影响。文献[19]研究了不同类型漏洞的生命周期演化过程，并提出了一个分布模型，用以计算漏洞在被可信网络安全信息商曝光后其利用难度与时间增长之间的变化趋势。CVSS 中记录的离散时间值难以作为生命周期因子来计算状态转移概率，因此，本文引入漏洞生命周期模型，使用文献[19]中的结果来定义攻击图中所利用漏洞的生命周期权重系数，并计算吸收马尔可夫链的状态转移概率矩阵P。通过计算漏洞的生命周期因子，结合攻击图分析其因果关系，综合漏洞生命周期的影响，评估网络的总体动态安全性。

定义5漏洞生命周期F(tv)。漏洞V的生命周期函数为

其中，tv为漏洞的有效生存时长，计算方式为漏洞曝光的日期与CVSS 对漏洞进行评分的日期之差；定义常量α和常量k为形状因子[19]，取值分别为0.26 和0.001 61。

STPVL算法综合考虑了漏洞的生命周期以及状态转移失败的情况，将攻击图转化成状态转移概率矩阵，其结果更具合理性且有助于安全研究人员在真实的网络环境下进行安全分析。STPVL 算法如算法1 所示。

算法1STPVL 算法

输入攻击图AG=(S,A,V,E)

输出吸收马尔可夫链的状态转移概率矩阵P

步骤1令i,j=1，Pi,j表示矩阵P中第i行第j列的元素。

步骤2从集合S中随机选择一个未遍历的节点Si。

步骤3令集合S′=S，从集合S中随机选取节点Sj，同时从集合S中删除所选节点Sj，即S={S-Sj}。

步骤4设节点Si的出度为m=0，查找攻击图中Si→Sj是否存在攻击路径Ei,,j及可利用漏洞Vi,j

ifEi,j存在

步骤6考虑将攻击失败时的状态转移看作节点到自身的一次转移过程，转移概率设为Pi,i。给出Pi,i的计算过程，设节点Si的出度为m

时间复杂度分析。假设共有n个状态节点，以一个n×n的矩阵P表示攻击图中的状态变迁，P中元素Pi,j的值表示节点Si到Sj的可达概率，在算法1中，首先，遍历n个状态节点的时间复杂度为O(n)。其次，每个节点都要遍历一次其他节点以判断两节点之间是否存在路径，若存在，则为Pi,j赋值；否则Pi,j=0，该过程需要n×n次遍历，时间复杂度为O(n2)，因此STPVL 算法的时间复杂度为O(n2)。

在STPVL 算法中，加入了随时间变化的漏洞生命周期，以此来计算攻击图对应的状态转移概率矩阵P，使其更贴合实际的网络环境。在吸收马尔可夫链中，状态节点最终到达吸收状态的概率总和为1，因此矩阵P中每一行满足

其中，Pi,j表示在生成的状态转移概率矩阵P中从状态节点Si转移到状态节点Sj的成功概率。

图2(b)是对图2(a)使用STPVL 算法处理后得到的吸收马尔可夫链攻击图，图中边上的数值表示状态转移概率。攻击路径S1→S2→S4对应的成功概率计算方式为E1,2E2,4=0.25×0.6=0.15。本文结合漏洞生命周期模型，根据目标网络拓扑中尚未修补的不同漏洞的生命周期，能够对攻击图中的脆弱点做出更准确的分析。通过对攻击者从初始状态开始的所有边上的可利用得分进行归一化，来计算吸收马尔可夫链的状态转移概率矩阵。为了确保模型的真实性，可以通过定时地更新状态转移概率矩阵中漏洞生命周期系数，重新计算状态转移概率矩阵P。

4 网络攻击分析

本文对网络攻击的分析基于状态转移概率矩阵的安全性分析，通过STPVL 算法得到攻击图对应的状态转移概率矩阵P后，以矩阵P为基础，引用其相关定理对目标网络的安全性进行全面分析，本节将依次对3 种网络攻击分析方法进行详细介绍。

4.1 节点访问频度分析

从任意状态节点出发，在到达吸收状态节点时，对其攻击路径上非吸收状态节点的访问次数期望被称为状态节点访问频度期望。下面，结合状态转移概率矩阵P与定理1 对其进行阐述。

定理1对于吸收马尔可夫链中状态转移概率矩阵P（如式(1)所示），记矩阵N为矩阵I-Q的逆矩阵，N=(I-Q)-1，N的大小为m×m。

矩阵N为攻击图的节点访问频度矩阵，N中元素Ni,j表示从状态节点Si出发到吸收状态时访问节点Sj的频度期望。Ni,j越大，说明在攻击图中，在到达目标状态节点途中经过该节点的次数越高，其威胁程度越大，需要提高其防护的优先级，状态节点访问频度指标在指导安全研究人员进行节点修复的环节中具有重要意义。

4.2 攻击路径长度分析

攻击路径长度用以衡量攻击者从初始状态节点开始，最终到达吸收状态时需要经过的预期步骤数。利用矩阵N可以计算从各状态节点到吸收状态的攻击路径的长度期望。

定理2假设攻击者以状态节点Si为初始状态节点，Ti为到达吸收状态所经过的路径长度的期望，T为第i个元素为Ti的列向量，则有

其中，T为攻击路径长度期望矩阵，N为攻击图的节点访问频度矩阵，c为单位矩阵，T和c均为列向量矩阵。

4.3 网络预期影响分析

网络的预期影响是结合单个漏洞的影响值与吸收马尔可夫链的状态转移概率矩阵共同构建的指标，通过控制漏洞生命周期的变化，推断出预期攻击成本随时间的变化趋势。对于单个漏洞的影响值Impact(v)，CVSS 提供了相关计算标准，计算式为

其中，C、I、A为CVSS 提供的3 种漏洞相关信息值，即保密影响、诚信影响和可用性影响，不同漏洞的具体数值公布在CVSS 官网中。对于随着漏洞生命周期变化的状态转移概率矩阵P，本文定义矩阵P(d)为每日状态转移概率矩阵，表示在漏洞曝光的第d天所计算出的攻击图的状态转移概率矩阵。矩阵P(d)中每一列元素值都代表攻击者利用漏洞vj从前一状态节点转移到节点Sj的概率，该漏洞的影响值为Impact(vj)，对Impact(vj)与P(d)中第j列元素的乘积求和，得到漏洞vj在第d天的利用成功概率，其他漏洞同理。因此，本文给出EI 的计算式为

其中，i和j分别表示状态转移概率矩阵中的行数和列数。

5 实验过程与分析

本节针对本文提出的基于吸收马尔可夫链攻击图的网络攻击分析方法进行实验及验证，实验过程与分析如下。首先，收集目标网络环境的拓扑信息、漏洞信息等，构建目标网络的一般攻击图；其次，通过STPVL 算法将一般攻击图映射为吸收马尔可夫链攻击图，并计算其状态转移概率矩阵；最后，通过第4 节中提出的3 种网络攻击分析方法对其分析验证。

5.1 搭建实验环境

为了验证本文方法的有效性，搭建了如图3 所示的实验网络拓扑环境，网络中的主要单位包括攻击者、外部防火墙和内部防火墙、路由器、Web 服务器H1和邮件服务器H2、办公区主机H3和H4，入侵检测系统（IDS,intrusion detection system）、主机H5和H6以及数据库H7。其中，外部防火墙隔离Internet 与内部网络，并将内部网络环境划分为3 个区域：隔离区（DMZ）、办公区、Intranet 区，而内部防火墙将DMZ 与其他内部网络区域相隔离。Intranet 区安置有IDS，并制定如下访问规则。

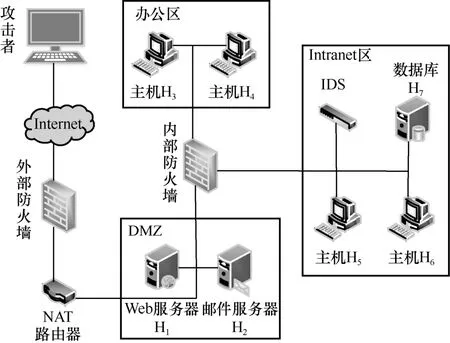
图3 实验网络拓扑环境

1) 外部防火墙仅允许来自Internet 的主机访问Web 服务器H1和邮件服务器H2。

2) 内部防火墙仅允许DMZ 中的主机访问办公区主机H3和H4。

3) Intranet 区中主机H5和H6仅能通过主机H3和H4访问。

4) 数据库H7仅允许Intranet 中的主机访问。

5.2 生成攻击图

首先，使用Nessus 漏洞扫描工具扫描实验网络环境，并结合NVD 官网信息，得到实验网络中各主机的漏洞信息，如表3 所示。其次，将网络拓扑和收集到的漏洞信息作为输入，利用攻击图生成工具Mulval 生成实验网络攻击图后进行简化，得到如图4 所示的实验网络环境攻击图。

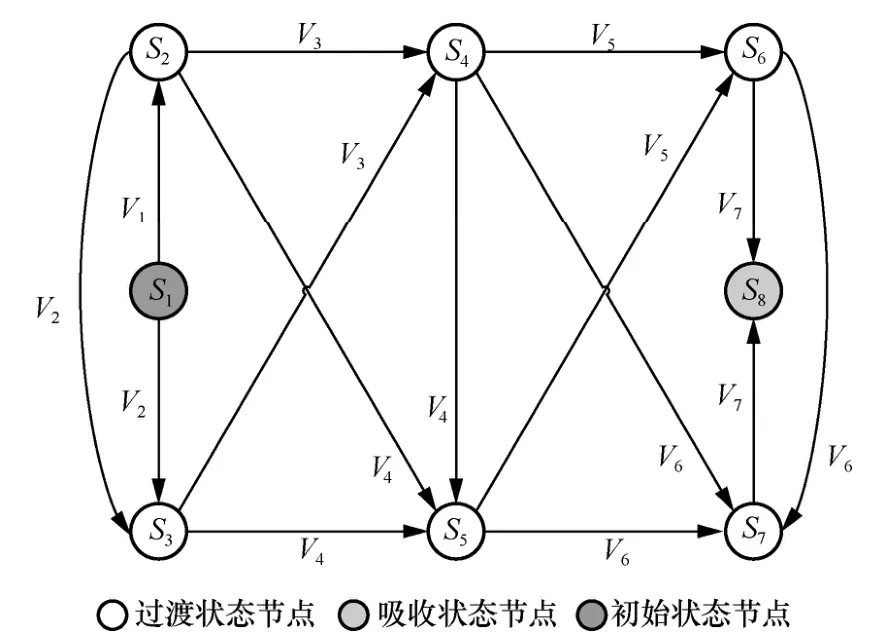
图4 实验网络环境攻击图

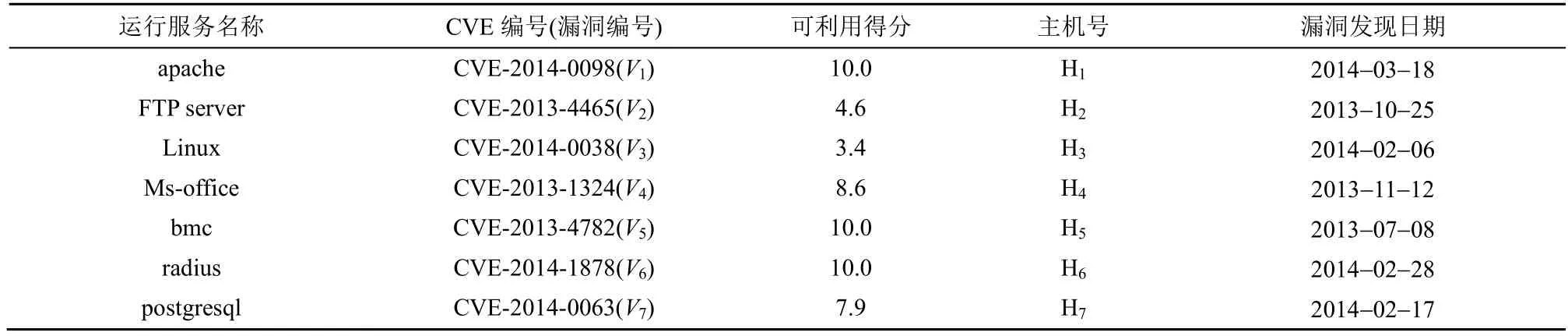
表3 实验网络中各主机的漏洞信息

图4 中，状态节点S1～S8表示攻击者不同时刻的状态，状态节点之间的有向边表示能够从边发出节点并跃迁至边指向节点，边上标注的漏洞V1～V7表示该状态转移过程所利用的漏洞序号。由图4 可知，攻击者处于初始状态节点S1，需要通过不同的攻击路径（状态转移过程）到达目标状态节点S8，最终获取目标数据库H7的最高权限。

5.3 攻击图到吸收马尔可夫链攻击图的映射

利用STPVL 算法，以图4 所示的攻击图为输入，通过算法映射得到吸收马尔可夫链攻击图，如图5 所示，并得到对应的状态转移概率矩阵P为

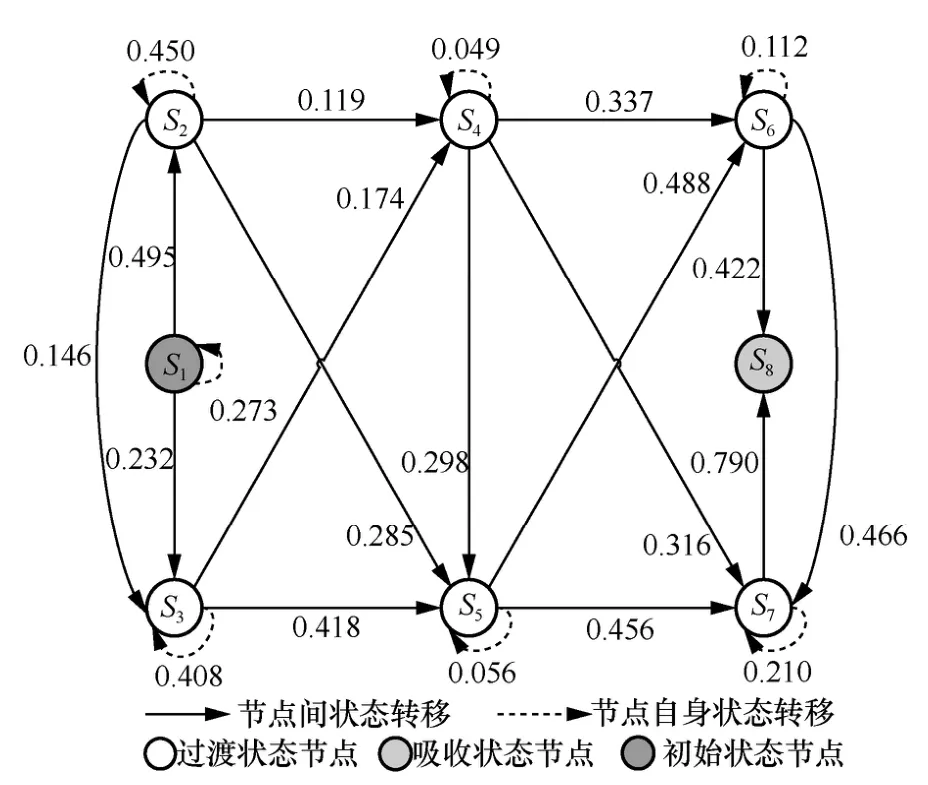
图5 吸收马尔可夫链攻击图

图4 和图5 中均含有8 个状态节点，S1表示攻击者初始状态节点，S8表示攻击者的目标状态节点，其余节点则表示过渡状态节点。

5.4 吸收马尔可夫链攻击图分析

5.4.1 攻击路径分析

定义6渗透成功概率。某条攻击路径上所有节点的状态转移概率的乘积为该路径的渗透成功概率PPn，可用于比较不同路径被攻击者选择的可能性大小，计算式为

其中，Pi,j为路径n上节点的状态转移概率。根据图5和其状态转移概率矩阵P，计算得到18 条完整的入侵路径，再利用式(8)计算出各路径的渗透成功率，具体分布如表4 所示。从表4 中可以看出，成功率最高的攻击路径为S1→S3→S5→S7→S8，其成功概率的计算式为P1,3P3,5P5,7P7,8=0.035。

表4 渗透路径长度及概率分布

通过使用上述方法，可以针对高危渗透路径Route4及时制定防御策略。同时，通过该方法得到的攻击路径分布能够辅助研究人员对可能发生的网络攻击做出相应的防御规划。

5.4.2 节点威胁程度分析

根据定理1 以及概率矩阵P进行计算，可以得到攻击图过渡状态概率转移矩阵Q和节点访问频度矩阵N

其中，矩阵N中的第一行表示攻击者从初始状态节点出发到吸收状态节点所经过的其他节点的期望次数。在攻击图中，访问频度越高的节点对应的威胁程度越高，对攻击者的重要程度越高，各个非吸收状态节点的访问频度期望如图6 所示。

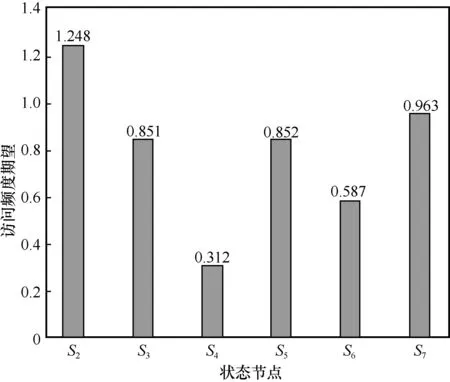
图6 非吸收状态节点访问频度期望

从图6 中可以看出，对于图5 中的各中间节点，其威胁程度排序为S2＞S7＞S5＞S3＞S6＞S4。因此，在对网络进行漏洞修复时，应优先修复主机H1上的apache 应用漏洞与主机H6上的radius应用漏洞。

该分析方法得到的节点访问频度期望能够有效评估攻击路径中节点的威胁程度，对指导安全研究人员进行攻击或漏洞修复具有重要意义。

5.4.3 攻击路径长度及网络预期影响分析

由定理2 和矩阵N计算可得，实验攻击图的攻击路径长度期望矩阵t为

矩阵t中元素表示从非吸收状态节点S1、S2、S3、S4、S5、S6、S7出发到吸收状态节点S8的攻击路径长度期望。该指标对检测攻击者的实时状态、规划攻防路线、分析攻击者下一步动向及预估攻击时长等具有指导意义。

图7 展示了攻击路径长度期望随时间的变化。从图7 中可以看出，在漏洞曝光后的300 天内，攻击路径长度期望整体呈下降趋势，这表明随着时间的增加，漏洞逐渐老化，漏洞的利用难度降低，攻击者采取的攻击步骤减少，攻击难度逐渐下降。这一规律总体符合实际情况，有利于安全研究人员预测后续攻击路径长度，为目标网络环境设置安全阈值，及时对网络系统中的漏洞进行修补。

图7 攻击路径长度期望随时间的变化

图8 展示了实验网络在300 天内预期影响的变化，预期影响代表了攻击者攻击所消耗的成本，即攻击代价。从图8 中可以看出，预期影响随时间的推移而降低，这表明将会出现更多影响值较低的漏洞，因此攻击者将会选择其他攻击难度较低的攻击路径。

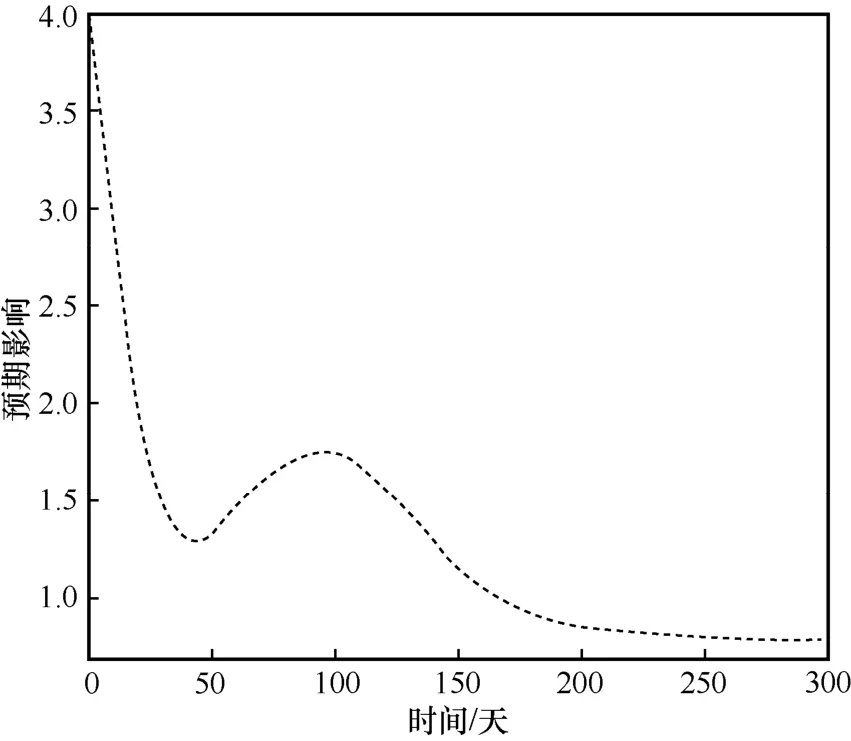
图8 实验网络在300 天内预期影响的变化

本文对攻击路径长度及网络预期影响的分析方法能够预测目标网络攻击路径长度的动态变化规律，以及网络环境的预期影响变化趋势。通过上述方法，安全研究人员可以实时地掌握攻击状态，在对网络进行安全补丁时更清晰地做出决策。

5.5 模拟实验与对比实验

5.5.1 攻击路径分布测试

实验1 为攻击路径分布测试的模拟仿真实验，在基于图3 的实验网络拓扑环境中，根据状态节点转移概率对攻击路径的选择进行建模，共进行1 000 次模拟攻击。实验系统使用Kali Linux，编程语言选择Pyhton3.6，网络拓扑及漏洞信息如表3 所示。

在模拟实验中，通过程序模拟攻击者原子攻击，从初始状态节点S1出发，以状态转移概率矩阵P中的元素为状态转移概率，模拟攻击状态之间的迁移，最终到达目标吸收状态节点S8后为一次完整的攻击。对1 000 次模拟攻击进行统计，成功到达目标状态节点S8的攻击次数为145 次，整体攻击成功率为=0.145，这与表4 中18 条路径渗透成功的概率总和0.132 4 相近，验证了本文方法的有效性。图9 为攻击成功的情况中次数最高的前10 条攻击路径分布。由图9 可知，最常用的攻击路径为S1→S3→S5→S7→S8，攻击路径长度为5，选择该攻击路径的次数在攻击成功次数中的占比为。

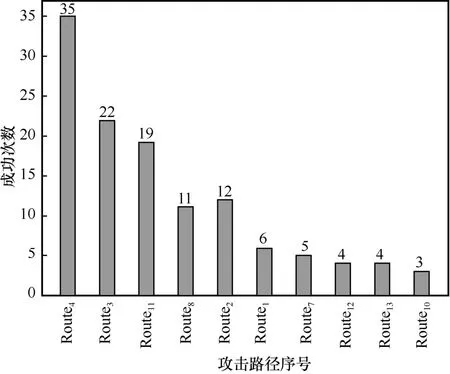
图9 攻击成功的情况中次数最高的前10 条攻击路径分布

由实验1 可知，各路径的选择频率与理论预期相符，再次证明了本文方法的合理性和有效性。

5.5.2 节点威胁程度变化趋势

实验2 为测试攻击图中各节点访问频度在不同漏洞曝光时长下的变化趋势的实验。漏洞曝光时长对节点威胁程度的影响如图10 所示。

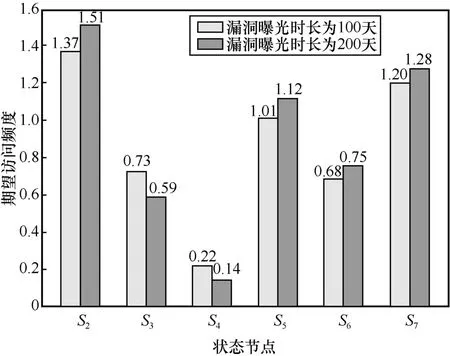
图10 漏洞曝光时长对节点威胁程度的影响

根据图10 中1 000 次模拟攻击对各状态节点的访问次数，在不考虑攻击者对初始状态节点以及目标状态节点的访问的前提下，对其进行分析。威胁程度最高的是S2节点，通过图5 和表3 可以判断，需要优先修复主机H1上的apache 服务漏洞，而对于S4节点对应的H3主机上的Linux 系统漏洞，可以适当降低它的修复优先级。从图10 中还可以看出，在漏洞曝光后的100～200 天，攻击者对状态节点S5的访问频度增加，但是对节点S3的访问频度减少，这表明在这段时间中，主机H4上bmc 漏洞的使用频率可能会增多，如果安全研究人员需要在这段时间内优先修复网络拓扑中某一漏洞，则可以根据以上信息，优先修复预期最容易受到攻击的主机节点。

由实验2 可知，本文方法通过分析节点威胁程度随漏洞曝光时长变化的趋势，可以为安全研究人员提供很有价值的信息，帮助其判断修复网络漏洞的优先顺序，并在分析网络安全性随时间变化的过程中做出更全面、更准确的决策。

5.5.3 对比实验

1) 与文献[11]方法对比

本文方法与文献[11]方法均基于CVSS 可利用得分来确定状态转移概率，然而CVE-2014-1878、CVE-2013-4782 的可利用得分均为10。在这种情况下，由于文献[11]没有考虑漏洞生命周期对状态转移概率的影响，导致其得到的结果不能反映真实的网络漏洞威胁程度。攻击路径中各节点的访问频度是网络环境安全评估的重要指标，为了证明本文方法的有效性，在图3所示的网络环境中进行对比实验，分别使用本文方法和文献[11]方法对图3 网络进行建模，并分析2 种方法所得的节点威胁度，如图11 所示。

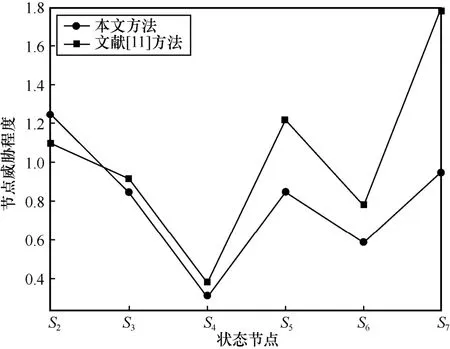
图11 2 种方法所得的节点威胁度对比

由图11 可知，2 种方法在S5、S7两节点上的访问频度存在较大差异。对文献[11]方法得到的节点威胁程度进行排序，可得S7＞S5＞S2＞S3＞S6＞S4，与本文方法得到的排序S2＞S7＞S5＞S3＞S6＞S4相比，可发现2 种方法得到的节点S2威胁程度存在较大差异。由表3 可知，虽然主机H1中漏洞V1的可利用得分与主机H6中漏洞V6可利用得分均为10，但是由于本文方法的漏洞生命周期较长，便于攻击者利用V1漏洞给予更高的威胁等级，导致上述差异。

本文方法在分析节点威胁程度时更具稳健性与准确性。本文方法得到的节点威胁程度排序与模拟实验中得到的结果相一致，表明本文方法更加符合实际网络环境，并且适用于对网络攻击的分析。

2) 与其他文献方法综合比较

从客观程度、是否进行漏洞生命周期度量、是否进行网络攻击分析3 个方面，将本文方法与其他方法进行对比，结果如表5 所示。从表5 中可以看出，文献[3]通过使用逻辑连接漏洞组成的攻击路径，将其扩展为攻击图，但并未对攻击图做进一步的分析；文献[7]构建了贝叶斯攻击图攻击分析模型，仅对攻击路径进行了预测；文献[11-12]使用马尔可夫链攻击图建模，但在对其分析时未考虑漏洞生命周期的影响；文献[16]结合漏洞生命周期过程，从宏观角度分析了漏洞状态的一般演化规律，但缺乏在网络攻击的分析中的应用。因此，可以得出以下结论。

表5 本文方法与其他方法综合比较

①本文方法具有高度客观性。本文方法构建了基于吸收马尔可夫链攻击图模型，并通过概率论的方法，从攻击路径、节点威胁程度、预期影响3 个方面对网络攻击进行分析评估，避免了网络攻击分析过程中主观因素带来的影响。

② 本文方法具有实用性。本文方法在计算攻击图状态转移概率矩阵时，融入了漏洞生命周期的影响，能够更真实地反映网络安全的风险情况，为网络安全研究人员提供更科学的决策支持。

③本文方法具有创新性。本文提出了一种基于吸收马尔可夫链攻击图的网络攻击分析方法，能够在客观条件下结合漏洞生命周期以概率论的方法对网络攻击进行分析，解决了其他方法中存在的客观性不足、计算攻击图概率转移时考虑不全面、没有对网络攻击进行全面分析等问题，具有创新性。

5.6 实验总结

1) 5.1～5.3 节使用本文方法对图3 实验网络进行映射，为后续实验提供分析依据。

2) 5.4 节从攻击路径、节点威胁程度、预期影响3 个方面对映射后的攻击图进行了详细的分析，为安全研究人员制定防御规划、修补漏洞以及掌握不同时期的网络安全状态提供了方法支撑。

3) 实验1 通过模拟实验，测试攻击过程中各路径的选择频率并与理论值相对比，证明了本文方法的有效性。

4) 实验2 通过预测不同漏洞生命周期下各节点访问频度的变化趋势，有助于安全研究人员了解网络中脆弱点的动态变化规律。

5) 对比实验首先将文献[11]方法与本文方法进行对比，表明在评估节点威胁程度方面，本文方法更具客观性和准确性。其次与其他方法进行比较，体现了本文方法的创新性与合理性。

本文方法以目标网络拓扑信息生成的攻击图为输入，通过概率论的方法对其进行分析，能够应用于公司、学校、政府等网络环境的分析，具有良好的扩展性。

6 结束语

攻击图技术能够直观地反映出网络的安全情况[20]，因此，对目标网络拓扑进行攻击图建模对于安全研究人员分析攻击者可能采用的攻击路径、及时制定防御措施具有重要的意义。针对现有基于吸收马尔可夫链构建攻击图的研究在对网络中状态节点转移概率计算时考虑因素不够全面的问题，本文提出了一种基于漏洞生命周期的状态转移概率归一化度量算法。该算法将目标网络的一般攻击图映射为吸收马尔可夫链攻击图，并给出其状态转移概率矩阵，通过该矩阵分析目标网络中潜在的攻击路径组合，计算预期攻击路径长度、节点威胁程度、预期影响，为网络管理人员提供详细指导。通过在实验网络上进行仿真分析，结果表明，本文方法能够客观地衡量目标网络环境中各项安全指标，并且能够有效预测攻击路径分布、节点威胁程度随时间变化的趋势，帮助安全研究人员更加准确地修复网络中的薄弱环节。如何评估未知漏洞及零日漏洞，以及给出合理度量其利用概率的方法，将是今后研究的主要工作。