（1.中国移动通信集团有限公司，北京 100032；2.中国移动通信有限公司研究院，北京 100053）

0 引言

面向2030 年，6G 将推动社会走向“数字孪生”和“智慧泛在”，实现虚拟世界和物理世界的融合交互[1]。智慧工业、智能交通、智慧医疗、智能交互等新兴业务场景的不断涌现，驱动着通信、计算、人工智能、大数据、安全等技术的深度融合[2]。除传统通信能力的提升之外，6G 网络还将打造与通信融合为一体的计算、感知、人工智能和安全等全新能力，以更好地支持未来全新的应用场景需求。在工业互联网、无人机、车联网等应用场景中，信息交互的维度已经从传统的信息传递扩展到信息采集、信息计算[3]，位置和目标感知能力和通信能力已经成为不可或缺的能力需求。所以，感知和通信的融合已经成为6G 研究的重要方向，而移动通信系统与雷达感知系统在信息处理流程、工作频段、大规模天线阵列应用等方面呈现出的高度相似性也为二者的融合提供了基础。

通信感知一体化技术通过传输信号一体化、硬件架构一体化等联合系统设计，可在同一套设备、同一段频谱上，同时实现通信与感知功能，带来设备成本降低、频谱利用率提升等增益[4]。一方面，通信感知一体化使基站具备通信、目标检测、高精度测距测速，以及目标成像和识别的能力，可以更好地满足众多全新应用场景的需求[5-6]，包括无人机、工业互联网和车联网等环境下的交通状态监控、低空状态监控、汽车对自动驾驶环境的感知、机器人之间的交互等。另一方面，感知信息反过来也可以用于辅助通信网络的部署与参数配置的优化。

通信感知一体化技术作为6G 的热点研究方向，学术界对其进行了大量的研究。文献[7-10]对通信感知一体化的发展以及未来研究趋势进行了详细的讨论，并从性能折中、信号处理、通信辅助感知、感知辅助通信四大方面阐述了通信感知一体化优势以及协作增益。针对智能交通及自动驾驶的场景，文献[11]对调频连续波雷达、多输入多输出（MIMO,multiple input multiple output）雷达、频率捷变雷达、正交频分复用（OFDM,orthogonal frequency division multiplexing）雷达等感知方式进行了充分的分析与对比。此外，针对无人机场景，文献[12-14]从无人机之间的通信与感知功能、无人机对地面物体的感知、移动网络与无人机之间的通信感知一体化等方面进行了详细的讨论。除了对应用场景、发展趋势与技术挑战的研究，针对通信感知一体化基础理论的研究是该方向的技术根基。相关学者对通信与感知一体化系统中的克拉美罗界进行了系统的推导[15-17]。此外，文献[18]针对通信感知一体化的信道，利用瑞利信息熵定义了感知的自由度，并以此来分析通信与感知一体化系统的分集增益。

基于现有蜂窝网络OFDM 波形进行通信感知一体化设计，实现对目标物体的感知，是目前通信感知一体化研究的技术路线之一，可最大程度降低对通信系统的设计和硬件的影响，具有更好的产业可实现性。本文研究将围绕这一技术路线展开。通过对收发端OFDM 信号进行联合处理，可利用周期图法得到感知目标的位置信息[4,19-20]。除了周期图法，文献[21-23]利用信号-噪声子空间分离的方法，可以得到目标物体的距离、速度、角度等信息。文献[24-25]对OFDM 通信感知一体化系统的功率分配、旁瓣干扰、峰均比等方面提出了对应算法并进行了优化。此外，针对射频硬件架构，文献[26-27]对功率放大器、频率合成器、混频器等进行了设计，并进行了实验与调测。针对单站感知的场景，文献[28]基于OFDM 信号进行系统设计，并针对收发间自干扰问题提出了射频与以及数字域的解决方案，并对静止目标以及移动目标进行了感知的外场测试。除了单站感知的方式，文献[23,29]等对多节点协作感知也进行了设计，并针对智能交通场景，利用OFDM 信号对汽车、行人等进行了感知定位。

值得注意的是，文献[19,23]在性能分析与系统设计时，侧重于算法在感知精度方面的性能，并未过多地讨论通信性能。文献[5,7-8]虽然考虑了通信感知一体化系统中的波束成形、帧结构、干扰管理等通信方面的设计，但是并未讨论感知资源与通信资源的分配问题。在通信感知一体化系统中，通信与感知性能相互耦合。一般而言，在总资源相同的情况下，用于感知的资源越多，通信性能下降越大。由于不同感知算法的感知精度、达到某一感知精度时所占用感知资源、计算复杂度不同，在通信感知一体化系统设计时，通信性能与感知性能的联合优化是十分必要的。

本文针对蜂窝通信感知一体化系统，以保障通信速率的同时实现感知精度提升为准则，对3 种基于OFDM 信号的多目标感知算法进行分析及优化设计，提出了一种自适应感知算法。该算法根据接收信号与干扰加噪声比（SINR,signal-to-interference-plus-noise ratio）测量结果选择合适的感知算法实现感知。相比使用单一算法，所提算法可保证在通信速率不变的情况下，实现感知精度的提升。本文主要创新点如下。

1) 介绍了3 种多目标感知算法，对算法的感知精度、感知资源占用情况及通信性能进行联合分析，并对感知算法的复杂度进行定量分析与对比。

2) 以保障通信速率不变的同时尽可能提升感知精度为优化准则，提出了一种自适应感知算法。

3) 在给定的系统参数下，通过链路级仿真平台验证高频通信感知一体化系统不同算法的感知性能及计算复杂度性能。

1 系统模型

如图1 所示，本文针对移动蜂窝网络，研究通信感知一体化技术的感知算法设计问题，利用现有蜂窝网络中规模部署的基础设施及网络架构，实现低成本、广覆盖范围的通信和感知。该通信感知一体化系统同时具备通信与感知功能，其中基站（BS,base station）在与用户进行数据传输的同时，可通过发射感知信号并接收对应的回波信号，完成未知目标的检测及距离与速度估计等感知任务。为减少/避免对现有移动通信网络硬件的大幅改造，本文考虑在现有移动通信网络基础上增加感知功能，即利用通信常用的OFDM 信号对未知目标进行估计。

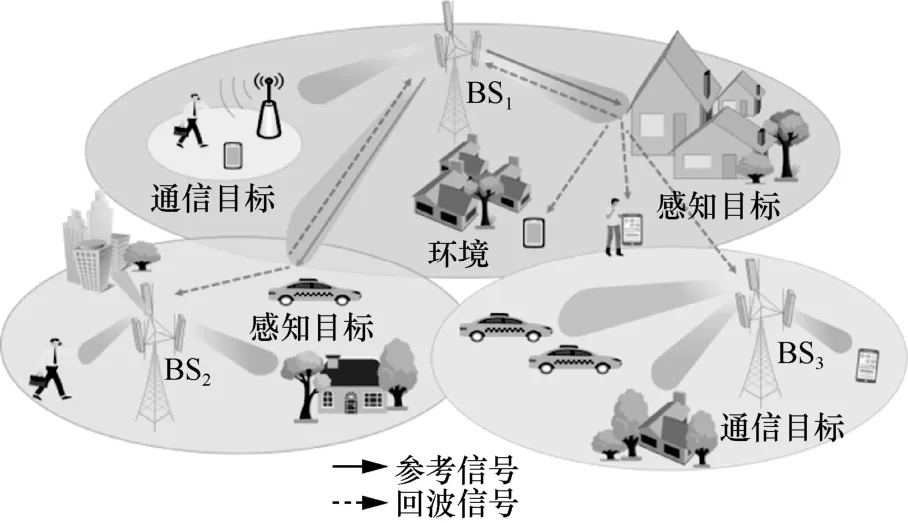
图1 通信感知一体化系统

对于每次感知，BS 发射用于感知的OFDM 信号，假设该信号由K个子载波和L个符号构成，子载波间隔为Δf，数据传输时长为。引入时间长度为TCP的循环前缀（CP,cyclic prefix）来对抗多径干扰，一个OFDM 符号的持续时间为TOFDM=T+TCP。因此，发射端用于感知的OFDM 基带信号表示为

其中，sl(k)为第k个子载波上第l个符号对应承载的调制符号；f k=kΔf为第k个子载波对应的频率；为方波，用于描述第l个OFDM 符号的矩形窗，其计算式为

OFDM 感知信号经过待测目标反射后到达接收端，经过匹配滤波、CP 删除和离散傅里叶变换等过程，接收端从基带接收信号中提取距离及速度信号。假设在BS 感知范围内有M个待测目标，第m个目标与基站的相对距离及相对速度分别为Rm和vm，则接收信号会在原始发射信号的基础上引入由传输时延及多普勒频移导致的相位差。因此，接收时域信号可表示为

其中，hm,k为信道增益，c为光速，λ为波长,n(t)为白噪声，服从均值为0、方差为δ2的高斯分布。

接收的时域信号经过傅里叶变换，得到频域信号可表示为

为便于观察，将发射端与接收端OFDM 符号分别整理成二维信号矩阵形式，如式(4)和式(5)所示。二维信号矩阵的每一行为一个子载波上的传输数据，每一列为一个OFDM 符号上的传输数据。

2 OFDM 多载波感知算法

2.1 2D-DFT 感知算法

二维离散傅里叶变换（2D-DFT,two dimensional-discrete Fourier transform）算法是较常见的OFDM 感知算法[20]，其核心是对时频域信道信息矩阵进行二维离散傅里叶变换，将时频域信道转换至时延多普勒域。然后通过对时延多普勒域的周期图谱进行谱峰搜索，估计感知目标与基站之间的时延及多普勒信息，进而得到目标物体的距离及速度信息。这种通过二维离散傅里叶变换将时频域信道转换至时延多普勒域的方法，使感知目标的时延及多普勒信息的展现更加直观。相比于直接处理时频域信道，2D-DFT 更易于实现高精度感知。

2D-DFT 算法的具体实现如下。令发射信号经过感知目标m反射至接收端时的传播时延为τm，多普勒为fD,m，将接收信号与发射信号进行点除，提取信道信息，得到信道转换函数Tdiv。

其中，FTx(k,l)及FRx(k,l)分别是第l个符号、第k个子载波上的基带发送及接收OFDM 信号，hm是第m个目标的信道增益，nk,l～CN(0,σ2)是加性白高斯噪声。当感知目标m和基站的距离为Rm时，对同一个OFDM 符号，每个子载波会经历时延。假设感知目标静止，则对于任意OFDM符号l，其对应的信道转换函数为

类似地，当感知目标m和基站的相对速度为vm时，对于同一个子载波，每一个OFDM 符号会经历线性频偏，该频偏是由多普勒频率引起的。若只考虑多普勒频偏，则对于任意子载波k，其对应的信道转换函数为

同样地，当式(11)中指数项抵消时，取到最大值。因此，对目标m=1,…,M，只需找到 {g(q) }q=1,…,Q峰值对应的索引qmax_index,m，即可求出目标速度vm为

根据上述分析，2D-DFT 算法的核心是对Tdiv的每列（即频率轴）做IDFT，并对每行（即时间轴）做DFT，得到其周期图谱并找到峰值，该峰值对应的二维索引即目标物体的距离和速度信息。周期图谱法如算法1 所示。

算法1周期图谱法

初始化感知子载波集K，感知符号集L，感知目标个数M

2.2 旋转不变子空间法

本节给出了一种基于旋转不变子空间[22]（ESPRIT）的感知算法，实现对感知目标的测距与测速。首先，将接收信号分成相位差相等且仅与时延相关的两组。该相位差被称为旋转不变因子。其次，通过对接收信号协方差矩阵进行估计，获得两组信号间旋转不变因子。最后，通过旋转不变因子与时延的关系对感知目标的时延进行估计。将OFDM 符号与子载波互换，采用相同算法可实现对感知目标多普勒的估计。

2.2.1 数据分组

将接收信号y(t)进行匹配滤波，可得到一组归一化基带OFDM 接收信号为

为噪声向量。式(13)可写为

为估计时延，将y拆分为y1及y2，使其各个对应元素间相位差相等且与除时延外其他未知量无关。例如，取y1为y的第一位至倒数第2 位元素，取y2为y的第2 位至最后一位元素。此时，y1与y2对应元素相位差为2πΔfτm。根据数学推导可得

其中，phase{a} 表示取元素a的相位。

2.2.2 旋转不变因子估计

本节给出基于ESPRIT 的估计算法。将向量y1与y2堆叠构成向量y3=((y1)T,(y2)T)T，将矩阵F1与F2堆叠构成矩阵F3=((F1)T,(F2)T)T，则有

其中，n3是对应的噪声向量。下面，本文算法将通过y1与y2估计旋转不变因子。为此，定义a的协方差矩阵为Ra，根据式(21)可得

其中，I是维数为2(K-1)×L的单位矩阵。定义Ra的前M个最大特征向量构成的特征矩阵为Ea。由于感知系统存在M个感知目标且式(21)成立，与F3分别扩张成了y3的信号空间。因此，存在一个非奇异矩阵T，使式(24)成立。

根据式(19)可得

式(25)表明旋转不变因子Φ是矩阵γ的特征矩阵，前者可由对矩阵γ进行特征值分解得到。因此旋转不变因子的估计可转化为对矩阵γ的估计。由于可由y1,y2,y3计算出，根据式(25)，通过最小二乘法，γ的估计值可由式(27)计算得出。

综合本节内容，ESPRIT 算法如算法2 所示。

算法2ESPRIT 算法

初始化感知子载波集K，感知符号集L，感知目标个数M

将接收信号的符号与子载波互换，采用相同算法即可得到对感知目标多普勒的估计。通过类似的理论推导，在进行多普勒估计时，旋转不变因子。在得到的估计之后，感知目标的估计速度由式(29)得出。

2.3 多重信号分类算法

多重信号分类（MUSIC,multiple signal classification）算法是一种经典的基于信号子空间和噪声子空间正交性的谱峰搜索算法[30]，已在角度估计中得到广泛应用。本节依据OFDM 系统中正交的子载波及符号与测向中阵元天线的相似性，进一步应用MUSIC 算法实现多目标的测速与测距，即如何利用MUSIC 算法获取目标的时延及多普勒信息。在算法实现过程中，将基于频域轴上等间隔的子载波构建时延导向矢量以获得待测目标的时延信息，类似地，将基于时间轴上等间隔的OFDM 符号构建多普勒导向矢量以获得待测目标的多普勒信息。

根据式(6)，进一步分析信道转换函数Tdiv可知，接收机与目标间的相对距离在连续子载波上的调制符号之间引入线性频偏，相对速度对应的多普勒频移在连续的OFDM 符号间引入线性相位。此外，时延及多普勒频移对调制符号造成的影响相互独立且正交。

下面基于相对距离及相对速度对调制域OFDM 符号影响的正交性实现时延及多普勒参数估计。首先，计算回波信号的协方差矩阵。根据上述分析，需要从Tdiv的每列及每行自相关矩阵中分别提取时延及多普勒信息，构造测距及测速协方差矩阵分别为

其次，基于协方差矩阵构建噪声子空间。将协方差矩阵RR与Rv奇异值分解，分别利用小特征值对应的特征矢量构建噪声子空间UR和Uv。

再次，构建感知信号导向矢量。根据发射信号的时频结构，可构建频域轴和时域轴对应的信号导向矢量，分别表示为

最后，进行谱峰搜索以获得目标的距离及速度。由于噪声的存在，噪声子空间与信号子空间并不完全正交，因此在计算时搜索式(4)的峰值，测距和测速的谱峰搜索式可表示为

将式(32)和式(33)中的R和v作为变量，通过对PR和Pv进行谱峰搜索来估计相对距离和速度。峰值对应的距离与速度即待测目标的速度与距离信息，可适用于多目标场景。对于基于MUSIC 算法实现的感知过程，其谱峰搜索过程中的搜索步长越小估计性能越好。综合本节内容，MUSIC 算法实现步骤如算法3 所示。

算法3MUSIC 算法

初始化感知子载波集K，感知符号集L，感知目标个数M

1) 输入收发OFDM 信号对应的二维信号矩阵，进行元素点除操作得到关于多待测目标的信道信息矩阵Tdiv；

2) 基于信道信息矩阵Tdiv构建测距协方差矩阵

3) 对协方差矩阵RR进行奇异值分解，并利用小特征值对应的特征矢量构建噪声子空间UR；

4) 根据发射信号的时频结构构建频域轴对应的信号导向矢量AR；

5) 以R作为搜索变量，对PR进行峰值搜索，获得M个峰值

6) 输出峰值对应的目标距离Rm,m=1,…,M。

类似地，利用多普勒相关测速协方差矩阵Rv与导向矢量Av，通过谱峰搜索即可估计感知目标的速度。

3 性能分析及自适应感知算法设计

本节首先从感知精度、感知资源占用情况及通信速率性能对上述3 种算法进行分析，然后比较3 种算法的计算复杂度。通过分析可得出单独使用上述3 种算法无法达到感知精度、通信速率及感知次数的最优。最后设计一种自适应算法，根据接收SINR 测量值的不同，切换不同感知算法，在占用通信资源数不变的情况下，达到感知精度的提升。

3.1 感知精度、感知资源占用情况及通信速率性能分析

首先，对3 种感知算法的感知精度进行分析。感知精度性能受限于克拉美罗界，总体来说，与感知资源个数、接收SINR 有关。定义γ为接收信号的SINR，根据文献[20,31-32]，采用2D-DFT 算法的估计误差与和二维离散傅里叶点数取值有关，采用ESPRIT、MUSIC 算法的估计误差与和信号空间的选择方法有关。结合文献[32]的分析结果，令2D-DFT、ESPRIT 及MUSIC 算法在关于接收SINR 收敛时的估计误差分别为EDFT、EESP和EMUS，满足

其次，从感知资源占用情况及通信速率性能的角度对3 种感知算法进行分析。由于2D-DFT 算法估计误差与有关，ESPRIT 及MUSIC 算法估计误差与有关，因此在达到相同感知精度时，2D-DFT 算法的最小接收 SINR 比 ESPRIT 及MUSIC 算法更低。令γDFT、γESP、γMUS分别为2D-DFT、ESPRIT、MUSIC 算法在成功感知目标且估计误差相同时所需最小接收SINR。根据文献[29]，在占用相同感知资源的情况下，为达到同一较低估计误差，3 种算法所需的最小接收SINR 满足

本文在图2 和图3 中分别展示了3 种算法在不同接收SINR 情况下的测距及测速均方根误差（RMSE,root mean square error）仿真结果。由图2和图3 可见，为达到相同RMSE，最小接收SINR越大，需要占用用于感知的资源越多。假设系统总资源数相同，使用2D-DFT 算法实现感知时，系统可用于通信的资源最多、通信速率最高，其次是ESPRIT 算法，最后是MUSIC 算法。例如，图3 表明，为达到2 m 测距精度（测距均方根误差为102m），2D-DFT、ESPRIT、MUSIC 算法所需的最小接收SINR分别为-26 dB、-24 dB、-22 dB。因此，为达到相同感知精度需求，相比于2D-DFT 算法，ESPRIT 与MUSIC 算法需要分别消耗1.5 倍及2.5 倍资源用于感知。假设系统采用2D-DFT 算法时资源用于感知，资源用于通信，则采用ESPRIT 和MUSIC 算法时，通信速率将分别减小25%及75%。

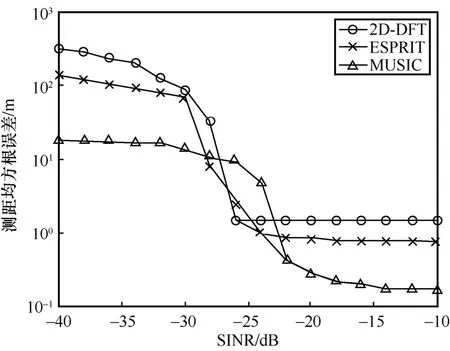
图2 3 种算法接收SINR 与测距均方根误差之间的关系

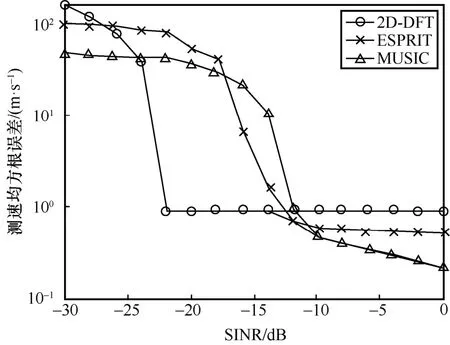
图3 3 种算法接收SINR 与测速均方根误差之间的关系

从上述对感知精度及通信速率的分析可以看出，在上述3 种算法中，尽管2D-DFT 算法感知精度最低，但是其通信速率最高；MUSIC 算法感知精度最高，但是其通信速率最低；ESPRIT 算法居于两者中间。

3.2 计算复杂度分析

本节对不同算法计算复杂度进行分析，用于定量比较不同算法理论上处理时延的大小。本文算法复杂度的影响因素主要包括快速傅里叶变换（FFT）和逆变换过程、协方差矩阵构造过程、奇异值分解过程、特征值分解过程、矩阵求逆过程、矩阵相乘过程、伪谱构造过程以及谱峰搜索过程等。其中，N点快速傅里叶变换及其逆变换的计算复杂度为Ο(NlogN)，假设向量为n维，矩阵为n×n维方阵，则向量与矩阵相乘的计算复杂度为Ο(n2)，矩阵乘法的时间复杂度为Ο(n3)。协方差矩阵构造过程涉及一次矩阵乘法则其计算复杂度同样为Ο(n3)；奇异值分解过程包括2 次矩阵乘法和2 次特征值分解，其中特征值分解的复杂度为 2Ο(n3)，总的计算复杂度为 6Ο(n3)；矩阵求逆的计算复杂度与矩阵乘法复杂度相同，为Ο(n3)；对于N点采样的频谱，其谱峰搜索的复杂度为Ο(logN)，对于MUSIC 算法，其每次谱函数的构造都是一次向量与矩阵相乘再乘以向量的过程，其计算复杂度可以视为2 次向量与矩阵相乘，为2O(n2)。3 种算法的计算复杂度如表1 所示。

表1 3 种算法的计算复杂度对比

以表2 为仿真参数的6G 高频通信感知一体化系统为例，当系统快速傅里叶变换点数为4 096 时，复杂度分析参数N= 4096，n=132，M= 4 096。从表1 可以看出，2D-DFT 算法复杂度最低，其次为ESPRIT 算法，MUSIC 算法复杂度最高。因此，尽管感知精度最低，在相同感知时间内，2D-DFT 算法感知次数最多，其次为ESPRIT 算法，MUSIC 算法最少。

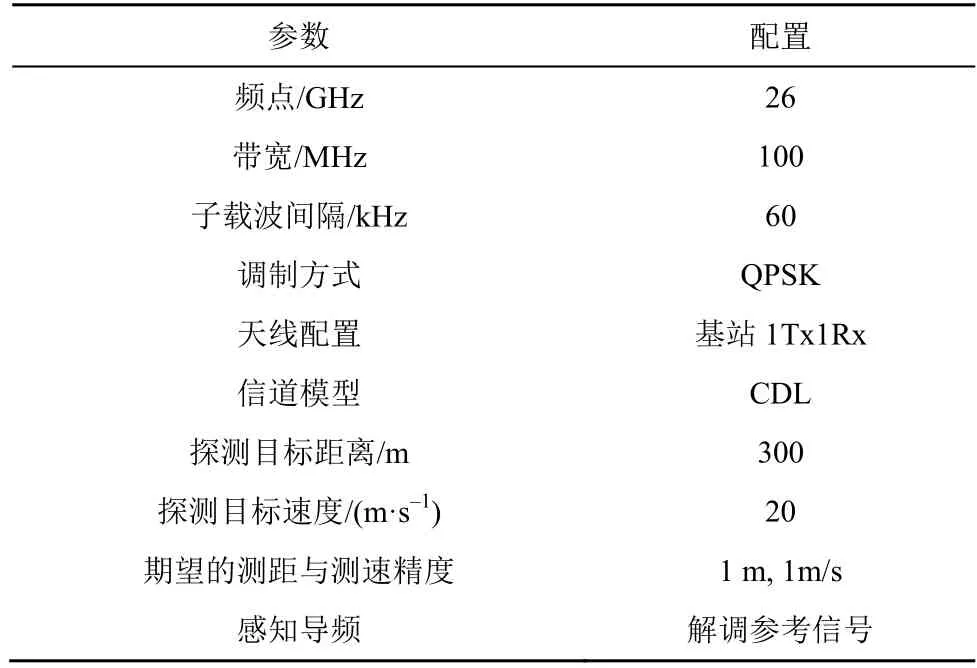
表2 链路级仿真参数及配置

3.3 自适应感知算法设计

从上述分析可知，感知精度较低的算法具有更高的通信速率及更低的计算复杂度。单独使用上述3 种算法均无法得到感知精度、通信速率及感知次数的最优。因此，有必要设计一种自适应感知算法，根据不同接收SINR 选择合适的算法实现感知，在相同通信速率的情况下，达到感知精度的最大化。

自适应感知算法具体操作步骤如下。首先，基站向环境中发射感知参考信号，参考信号被感知目标反射后形成回波被基站处的感知接收机接收。然后，基站对回波信号的接收SINR 进行测量，根据不同SINR 的取值从2D-FFT、MUSIC 及ESPRIT中选择一个合适的算法，使系统的感知精度最高。

根据式(37)中3 种感知算法在达到较低估计误差时最小接收SINR 的关系，定义θ0＜θ1＜θ2＜θ3为感知算法的切换阈值，可由先验仿真或者系统实际测试得到。以最小化感知参数最小均方误差为目标，根据图2 所示的仿真结果，自适应感知算法在不同SINR 情况下的选择准则如下。

1) 当γ＜θ0时，感知算法误差大，感知失败，默认采用2D-DFT 算法测距；

2) 当θ0≤γ＜θ1时，采用2D-DFT 算法测距；

3) 当θ1≤γ＜θ2时，采用ESPRIT 算法测距；

4) 当γ≥θ2时，采用MUSIC 算法测距。

针对目标测速问题的自适应感知算法与测距相似。综合本节内容，自适应感知算法如算法4 所示。

算法4自适应感知算法

初始化感知子载波集K，感知符号集L，感知目标个数M，算法切换阈值θ0、θ1、θ2、θ3

4 仿真结果

为减少/避免对6G 通信基本链路和性能的影响，本文考虑利用通信常用的OFDM 信号进行通信业务传输以及对未知目标的参数估计。在未知目标参数估计过程中，为评估2D-DFT、ESPRIT、MUSIC 及自适应感知算法在实际移动通信系统下的感知性能，本节基于时分双工（TDD,time division duplexing）移动通信系统以及宏蜂窝（UMA）应用场景展开，采用物理下行共享信道（PDSCH,physical downlink shared channel）进行链路级仿真评估，信道模型为簇延时线模型（CDL,clustered delay line）。仿真参数如表2 所示，通信感知一体化工作频段为26 GHz，带宽100 MHz，探测目标距离为300 m，探测目标速度为20 m/s。仿真过程中采用解调参考信号（DMRS,demodulation reference signal）作为感知导频，可在不影响通信吞吐的前提下实现目标感知，通信数据和感知导频映射方式如图4 所示。

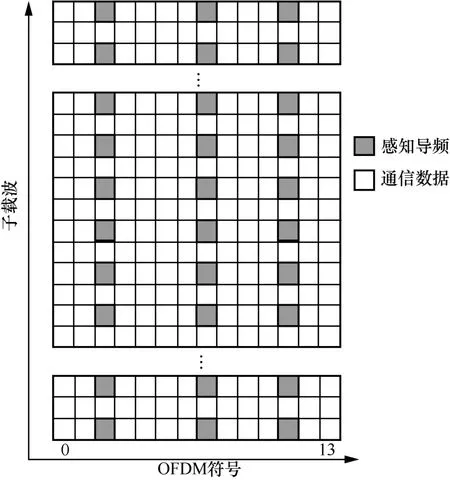
图4 PDSCH 中通信数据和感知导频映射方式

链路级仿真性能评估的主要评价指标包括测距精度和测速精度，通过500 次蒙特卡罗仿真获得。感知精度由参数估计值与真实值的最小均方根误差刻画。令待估参数测量次数为Nsamp，待估参数真实值为θ，第i次估计值为，RMSE 计算式为。

图5 对比分析了4 种算法的测距性能。从图5中可以看出，4 种算法的测距精度在不同SINR 下呈现差异性。当接收SINR＜-26 dB 时，4 种算法测距误差较大，此时感知失败。当接收SINR≥-26 dB 时，随着SINR 的增加，4 种感知算法感知精度逐渐降低。当感知精度收敛后，2D-DFT、ESPRIT、MUSIC 算法测距精度分别为1.45 m、0.76 m、0.17 m。当达到1 m 测距精度（测距均方根误差为101m）时，ESPRIT和MUSIC算法的接收SINR分别为-24 dB和-22 dB。相比上述3 种算法，在感知成功的情况下（接收SINR≥-26 dB），自适应感知算法的估计误差曲线不高于其他任一感知算法误差曲线，表明其测距精度为4 种算法中的最优。

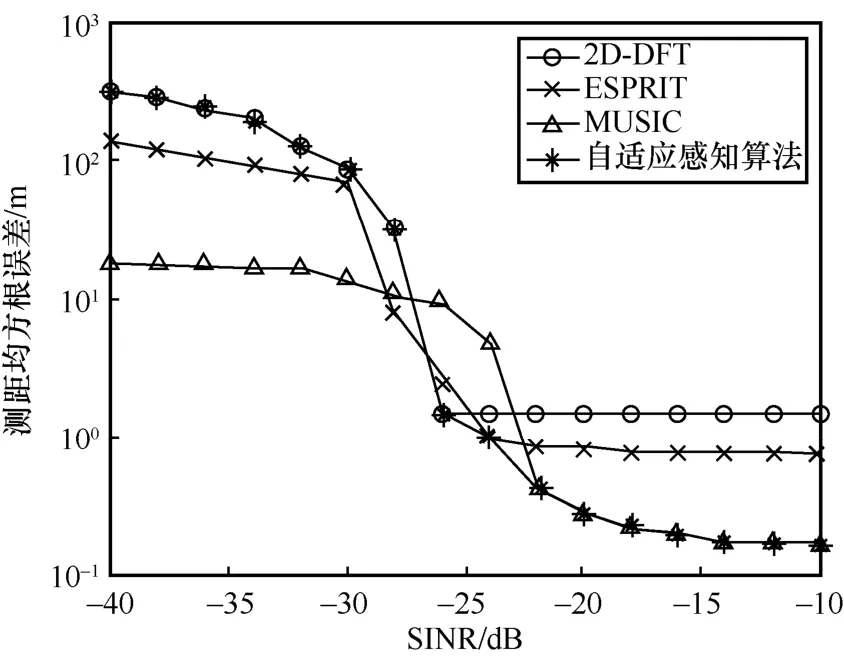
图5 4 种算法接收SINR 与测距均方根误差之间的关系

图6 对比分析了4 种算法的测速性能。当接收SINR＜-22 dB 时，4 种算法测速误差较大，此时感知失败。当接收SINR≥-22 dB 时，与测距结果类似，随着接收SINR 的增加，4 种感知算法测速精度逐渐降低。当测速精度达到1 m/s（测速均方根误差为101m/s）时，2D-DFT、ESPRIT、MUSIC算法接收SINR 分别是-22 dB、-13 dB、-12 dB。算法收敛后，2D-DFT、ESPRIT 算法测速估计误差分别为0.92 m/s、0.53 m/s。与前两者不同，MUSIC 算法随着SINR 的提升，测速估计误差可进一步降低。相比上述3 种算法，在感知成功的情况下，自适应感知算法测速估计误差曲线不高于其他任一感知算法误差曲线，表明其测速精度优于上述3 种算法。

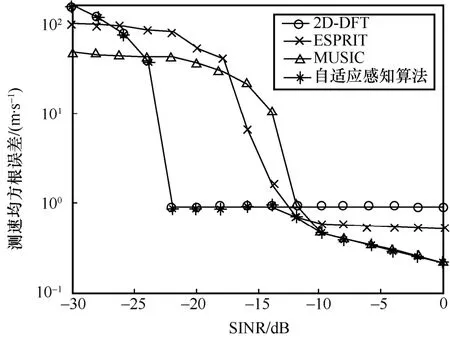
图6 4 种算法接收SINR 与测速均方根误差之间的关系

图7 描述了4 种算法在达到期望的探测精度（1 m 测距精度、1 m/s 测速精度）时所对应的最大通信速率增益。由于不同感知算法在达到同一感知精度时对接收SINR 的要求不同，系统需要配置不同数量的资源用于感知。在感知与通信总资源相同的情况下，不同感知算法对应的通信速率不同。在测距方面，自适应感知算法与ESPRIT 算法实现感知的通信速率相同，且通信速率最高。MUSIC 算法通信速率比ESPRIT 算法下降60%。由于2D-DFT算法无法达到1 m 的测距精度，设定系统分配所有资源用于感知，因此通信速率为0。在测速方面，自适应感知算法与2D-DFT 算法通信速率相同，ESPRIT 次之，MUSIC 最低。综合比较测距与测速时的通信速率可知，所提出的自适应感知算法的最大通信速率增益优于其他3 种算法。

图7 不同算法在达到期望的探测精度时的最大通信速率增益

为评估算法计算复杂度，表3 进一步对比分析了3 种算法的运行时间。仿真过程采用16 核Intel(R) Xeon(R) W-2245 CPU 工作站进行运算。以图5 测距性能分析为例，2D-DFT、ESPRIT、MUSIC 这3 种算法的运行时间分别为2.4 ms、856.4 ms、9 708.7 ms，与第3 节理论分析结论一致。对比上述算法及自适应感知算法，自适应感知算法复杂度始终不高于MUSIC，且仅在接收SINR≥-26 dB测距（或SINR≥-12 dB 测速）及接收SINR≥-22 dB测距（或SINR≥-10 dB 测速）时分别高于2D-DFT及ESPRIT。结合图3 和图4 可知，由于自适应算法感知误差更低，其较高的计算复杂度是可接受的。

表3 不同感知算法在测距时的运行时间

综合上述分析可知，2D-DFT 具有最低收敛SINR、低复杂度的优势，但其测距或测速精度受限，而ESPRIT、MUSIC 可在较高SINR 条件下达到期望的测距和测速精度需求，但其代价是较高的计算复杂度。因此，面向6G 融合多元化的应用场景，可综合精度需求、计算复杂度等因素灵活选取或切换不同感知算法，满足不同应用场景下的需求。例如，对于精度要求不高，或感知时延敏感，或设备处理能力受限的场景，可优先采用2D-DFT 算法。对于精度要求较高，或感知时延不敏感，或设备处理能力较强的场景，可进一步考虑ESPRIT、MUSIC 算法。通过灵活选取或切换算法，实现感知性能与复杂度较好的折中。

5 结束语

本文研究基于OFDM 波形的通信感知一体化融合算法设计及优化，首先给出了基于OFDM 波形的通信感知一体化系统模型，介绍了3 种可实现多目标测距与测速的感知算法，并进行了相应的感知精度、感知资源占用、通信速率及计算复杂度的分析，可以看出单独使用任一算法均无法达到感知精度、通信速率及感知次数的最优。基于上述分析，本文提出了一种自适应感知算法，在实际系统中，接收端通过对接收SINR 的测量选择合适的感知算法实现感知，在通信速率不变的情况下，可实现对感知精度的提高。最后，本文通过链路级仿真验证了感知算法的感知精度及计算复杂度。值得注意的是，除现有OFDM 波形外，6G 通信感知一体化系统还可引入新型波形实现系统性能的提升。基于新型波形技术的感知与通信性能联合分析及方案设计将在未来的工作中研究。